�ĤQ�� �t���ݭȪk
�t���ݭȪk(Method of Weighted Residuals, MWR)�����[���A�O�Q�Τ@�զh�������ܪ������D�����T�ѡA�N���T�ѻP����Ѫ��~�t�ݭȡA���H�A�����t����ƫ�A�Ϩ��`�M�οn���ȳ̤p�ơA�H�F��̱��T�Ѫ��ؼСC�u�{�ɱĥ�MWR�t���ݭȪk�ѨM�u�{���R���D�A����1960�~�N�}�l�A�ثe�w���\�h�M�� [ 1�A2�A3 ] �ԲӰQ�׳o�ؤ�k�A�����μs����y��O�ǡB���ǻ��B��q�ǻ��B�����u�{���U���A�O�@�ج۷����IJv���ƾǤu��C�t���ݭȪk���A�S�H�ƾǰt�m�k�̩���ϥΡA��~�Ӥw�����ѷL����{�����ƭȤ�k���̼s�x�Q�ϥΪ���k���@�C
�Ĥ@�` �t���ݭȪk��z
���F�����t���ݭȪk���Q�k�P�B�z��k�A�ڭ̭����H�@�ӳ�²�檺��ɭȱ`�L����{�����ҥ[�H�����C
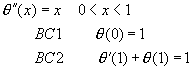 (10-1.1)
(10-1.1)
���]![]() ��
��![]() �b0��x��1���϶������O�s���ơA�h�H�W��{�����Ѥ]���M�O�@�ӳs���ơC�ھڥ��ѲĤT���������A����s���Ƴ��i�H�Q�Τ@�Ӧh�����ӥN���Q�]���A��{��(10-1.1)���ѡA�i�H�Q�Τ@�L���żƪ��M���ܤ��C
�b0��x��1���϶������O�s���ơA�h�H�W��{�����Ѥ]���M�O�@�ӳs���ơC�ھڥ��ѲĤT���������A����s���Ƴ��i�H�Q�Τ@�Ӧh�����ӥN���Q�]���A��{��(10-1.1)���ѡA�i�H�Q�Τ@�L���żƪ��M���ܤ��C
![]()
�䤤ui(x)�٬���¦���(Basis Function)�C�ѩ�x���d��0��x��1�A��i�ȼW�j�ɡAxi�Y�ֳt�ܤp�Q�]���A���F²�ư_���A�Ҽ{��i > N��xi�Y�i�����A ![]() �i�H���]���Q�Τ@��(N��1)���h����������C
�i�H���]���Q�Τ@��(N��1)���h����������C
![]() (10-1.2)
(10-1.2)
�ѩ�![]() ����{��(10-1.1)������ѡA�]���A
����{��(10-1.1)������ѡA�]���A![]() �]�n�����L����{���������ɱ���ABC1��BC2�F�N
�]�n�����L����{���������ɱ���ABC1��BC2�F�N![]() �N�J��ɱ���BC1���A�o��G
�N�J��ɱ���BC1���A�o��G
BC1 ![]() (10-1.3)
(10-1.3)
�N![]() �N�J��ɱ���BC2���A�o��G
�N�J��ɱ���BC2���A�o��G
BC2 ![]()
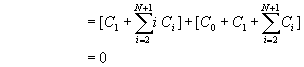
�αN����{����z��o��
![]() (10-1.4)
(10-1.4)
�N��{��(10-1.3)��(10-1.4)�N�^��{��(10-1.2)�A�h�c������Ѫ��ܦ��i�H��g����
![]() (10-1.5)
(10-1.5)
����{�����t��C2�AC3�A�K�K�ACN��1�`�@N�ӥ��w�Y�ơA�]���A�ݭn�A�Q��N�Ӻ����L����{��(10-1.1)������ӨM�w�o�ǫY�ơC
���F²�ƻ����_���A�����Ҽ{N��1�����p�A��Y![]() �A�h��{��(10-1.5)�i²�Ʀ�
�A�h��{��(10-1.5)�i²�Ʀ�
![]() (10-1.6)
(10-1.6)
�H�W�B�J���إ߷L����{������Ѫ��ܦ�����k�C�䦸�n�Ҽ{�p��M�w���w�Y��C2�AC3�A�K�K�ACN��1�C���F²�ƻ����_���A�N�L����{���g��L{x�Ay}��0���Φ��Q�Y����h����(10-1.2)����������L����{���A�h�N�J�L����{���N�o��L{x�A![]() }��0�C���ѩ�p�e���һ���
}��0�C���ѩ�p�e���һ���![]() ������ѡA�N
������ѡA�N![]() �N�J�L����{��L{x�Ay} ���A���G���@�w��o��s�C�]���A�w�q
�N�J�L����{��L{x�Ay} ���A���G���@�w��o��s�C�]���A�w�q![]() �N�J�L����{���ұo�쪺�ݭȬ�R��L{x�A
�N�J�L����{���ұo�쪺�ݭȬ�R��L{x�A![]() }�C
}�C
�N��{��(10-1.6)�N�J���{���A�o��ݭȬ�
![]() (10-1.7)
(10-1.7)
�Y![]() �����T�ѡA�h�ݭ�R��0�C���Ѥ�{��(10-1.7)�i�H���D�A�ѩ�x���0�P1��(0��x��1)�A�]���A�ڭ̭Y��w�Y�@�S�wC2�ȡA����ϴݭ�R�b0��x��1�����Y�@�I�ɬ��s�A�Ӧb��Lx��m���ݭ�R�h�i��j��Τp��s�C�i�O�ݪ`�N�ѩ�
�����T�ѡA�h�ݭ�R��0�C���Ѥ�{��(10-1.7)�i�H���D�A�ѩ�x���0�P1��(0��x��1)�A�]���A�ڭ̭Y��w�Y�@�S�wC2�ȡA����ϴݭ�R�b0��x��1�����Y�@�I�ɬ��s�A�Ӧb��Lx��m���ݭ�R�h�i��j��Τp��s�C�i�O�ݪ`�N�ѩ�![]() �u�O�@�Ӫ���ѡA�p�G�ݭ�R�b�C�@x��m������s�A���M�O�̦n���ѵ��A�_�h�]�i�H�h�ӨD�䦸�A�n�D�ݭ�R�b�ҦҼ{�϶�0��x��1�����Y�@�إ����Ȭ��s�A��Y�A���ݭ�R���t���n�����s�A�礣�����@�}�n������ѡC�o���[���H�ƾǦ����ܡA�Y��
�u�O�@�Ӫ���ѡA�p�G�ݭ�R�b�C�@x��m������s�A���M�O�̦n���ѵ��A�_�h�]�i�H�h�ӨD�䦸�A�n�D�ݭ�R�b�ҦҼ{�϶�0��x��1�����Y�@�إ����Ȭ��s�A��Y�A���ݭ�R���t���n�����s�A�礣�����@�}�n������ѡC�o���[���H�ƾǦ����ܡA�Y��
![]() (10-1.8)
(10-1.8)
��Y�A�u�n���w�t�����![]() �A�Q�Τ�{��(10-1.8)����n����A�Y�i�D�ѥ��w�Y��Ci�C�M��A�N�^
�A�Q�Τ�{��(10-1.8)����n����A�Y�i�D�ѥ��w�Y��Ci�C�M��A�N�^![]() �����ܦ�(10-1.2)�A�Y�i�D�o�L����{���������
�����ܦ�(10-1.2)�A�Y�i�D�o�L����{���������![]() �C�H�W�һ������N�O�t���ݭȪk���Q�k�P�B�J�A�[�H��z�p�U�G
�C�H�W�һ������N�O�t���ݭȪk���Q�k�P�B�J�A�[�H��z�p�U�G
(1) �Q�Τ@�Ӧh����![]() �@���L����{��L{x�Ay}��0������ѡF
�@���L����{��L{x�Ay}��0������ѡF
(2) �Ϧh���������L����{������ɱ���A��²��![]() ���ܦ��Q
���ܦ��Q
(3) �N�J�L����{��L{x�Ay}��0�A�D�X�ݭȪ����ܦ�R��L{x�A![]() }�Q
}�Q
(4) �w�q�t�����![]() �F
�F
(5) �ϰt���ݭȪ��n�������s�A�Y![]() �Q�i�H�إ�N�ӥ��w�Y��Ci���p�ߤ�{���F
�Q�i�H�إ�N�ӥ��w�Y��Ci���p�ߤ�{���F
(6) ���p�ߤ�{���A��X����h���������w�Y��Ci�Q
(7) �N�^�����h����![]() �A�إ߷L����{��������ѡQ
�A�إ߷L����{��������ѡQ
(8) �Q�ξA�������k�A�p��L����{���b�S�w��m���ѡC
�t���ݭȪk(Methods of Weighted Residuals)���Q�k�p�e�������СA���t�����![]() ���h�ؤ��P����ܡC�̩ҿ�ܰt�����
���h�ؤ��P����ܡC�̩ҿ�ܰt�����![]() �����P�A�������t���ݭȪk�Y�����P���W�٤Τ��P���S�ʡA�H�U���O²�n���Ф��C
�����P�A�������t���ݭȪk�Y�����P���W�٤Τ��P���S�ʡA�H�U���O²�n���Ф��C
[A] �t�m�k(Collocation Method)
�t�m�k���t�����![]() �w�q��
�w�q��
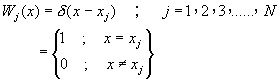 (10-1.9)
(10-1.9)
�䤤![]() �٬��t�m�I(Collocation points)�C
�٬��t�m�I(Collocation points)�C![]() �٬�Dirac Delta��ơA���]�ݭ�R��L{x�A
�٬�Dirac Delta��ơA���]�ݭ�R��L{x�A![]() }��Ʀb�ҦҼ{��������nV���~���s�b�A�h�t���ݭȿn�����i�H�g��
}��Ʀb�ҦҼ{��������nV���~���s�b�A�h�t���ݭȿn�����i�H�g��
![]()
�o�ؤ�k���ܦb�t�m�I��m�W���ݭȤ@�w���s�C��N�ȼW�j�ɡA�ݭ�R(x)�|�b�V�h���I�W���s�A�ϱo������ͪ���ڸѡC
���Y��(Lanczos, C. 1938)��ܮ�Ҧh����(Chebyshev Polynomial)�@����¦���ui(x)�A��Ҧh�����O�@�إ���h�����C���Y���çQ�ή���Ҧh�������ڧ@���t�m�I�A�o�ؤ�k�Y�٬�����t�m�k(Orthogonal Collocation)�C
[B] �ڿդ��X���Ǫ��k(Bubnov-Galerkin Method)
�b�t���ݭȪk���̦��W����k�A�i��N�O�ڿդ�--���Ǫ��k�C�b�o�ؤ�k���A�w�q�t�����![]() ����¦���uj(x)�良�w�Y��Cj���ɨ�ơA�H�ƾǦ����ܬ�
����¦���uj(x)�良�w�Y��Cj���ɨ�ơA�H�ƾǦ����ܬ�
![]() (10-1.10)
(10-1.10)
�b�o�ؤ�k���Auj(x)���@�հ�¦��Ƥ��@�A�ϱo�b�ҦҼ{������n���A�����Ƴ��i�H�Q�γo�հ�¦��ƪ��ܤ��A![]() �C�]���A��N�ͪ��L�a�j�ɡA����Ѧb�ҦҼ{���Ŷ����Y��N�����T�ѡC
�C�]���A��N�ͪ��L�a�j�ɡA����Ѧb�ҦҼ{���Ŷ����Y��N�����T�ѡC
[C] �����X���ڼw�̤p����k(Gauss-Legendre Least Square Method)
�����X���ڼw�̤p����k�����[���A�O�Q�δݭȪ�����n�������s�A��X���ݭȳ̤p�ƪ����w�Y�ơC![]() �C��Y�A
�C��Y�A
![]()
�ѥH�W���Y���A�i�H�إ�N�եN�Ƥ�{���C�o�ؤ�k���㦳�ƾǷN�q�A�z�פW�O�j�����~�t�ȱo����M�F�̤p�ơC�ѤW�@��{���A����t����Ƥ��w�q�A�i���o�ؤ�k���t�����![]() ��
��
![]() (10-1.11)
(10-1.11)
�̤p����k�b�\�h�u�{���ΤW�`�Q�ϥΡA���ѩ�ϥδݭȪ�����n�����A�]�ܮe�����ͫܧx�Z���N�Ƥ�{���C
[D] �D�q�k(Method of Meoments)
�D�q�k�̥��Q���Φb�D�u�ʺ��z(Non-linear Diffusion)�άy��O�Ǥ����h�y��ɼh(Laminar Boundary Layer)���D���ѪR�W�A�W�n�D�ݭȪ��s���D�q���s�C��Y�t����Ƭ�
![]() (10-1.12)
(10-1.12)
�Ĥ@������D�q�k�����G�A�P�Ҽ{��Ӱ϶������@�Ӥl�϶����϶��k�ۦP�A�o�ت���k�b�h�y��ɼh���D���ѪR�W��٬����d���������˪���k(von
Karman & Pohlhausen Similarity)�C
[E] �ư϶��k(Subdomain Method)
�ư϶��k�O�N��Ӫ��϶�(0�A1)���Φ�N�Ӱư϶��A�éw�q�t����Ƭ�
 (10-1.13)
(10-1.13)
��10-1
�t���ݭȪk
�էQ�ΦU�ؤ��P���t���ݭȪk����ɭȱ`�L����{��(BVP-ODE)
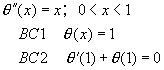
���G���T�Ѭ�![]()
[��]
[A] N��1�F![]() �F�ݭȪ��ܦ���
�F�ݭȪ��ܦ���
![]()
![]()
�ھ�MWR����z�G![]() �A�H�U�H�U�ؤ��P�t����ơA�إߥ��w�Y��C2���ȡC
�A�H�U�H�U�ؤ��P�t����ơA�إߥ��w�Y��C2���ȡC
(i) �t�m�k�G�t����Ƭ�W�ף_(x��x1)
�O�t�m�Ix1��0.5�Q�oR��2 C2��0.5��0�A�YC2��0.25�A�����Ƭ�
![]()
�Y�Ox1��0.6�Q�h�oC2��0.3�C�����Ƭ�
![]()
�`�N�G�t�m�k�ұo���G�|�]�t�m�I��m����ܦӲ��C
(ii) �ڿդҡи��Ǫ��k�G�t����Ƭ�![]()
![]()
�G![]() �F�@
�F�@![]() �C
�C
(iii) �̤p����k�G�t����Ƭ�![]()
![]()
�G![]() �F �@
�F �@![]() �C
�C
(iv) �D�q�k�G�t����Ƭ�![]()
![]()
�o��![]() �F �@
�F �@![]() �C
�C
(v) �ư϶��k�G�t����Ƭ�W(x)��1�F0��x��1
![]()
�o��![]() �F �@
�F �@![]() �C
�C
[B] N��2�F�Ҽ{�G�������ơA�Y��N=2�Q�Ѥ�{��(10-1.5)�o�G������Ѭ�
![]()
�N�^��L����{���A�o��ݭȬ�![]()
![]()
(i) �t�m�k�G�t����Ƭ�![]() �Fj��1�A2
�Fj��1�A2
�O�t�m�I��![]() ��
��![]() �Q�h�o�t�m�I�ݭȬ�
�Q�h�o�t�m�I�ݭȬ�
![]()
![]()
�Ѥ��A�o![]() �A�B
�A�B![]() �A�N�^������Ƥ�{���A�o��L����{�����G������Ѭ�
�A�N�^������Ƥ�{���A�o��L����{�����G������Ѭ�
![]()
�P���T�ѬۦP�C
(ii) �ڿդҡи��Ǫ��k�G�t����Ƭ�![]()
![]()
![]()
�t���n�����i�H�������
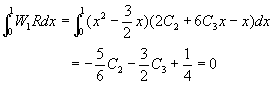
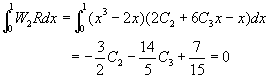
�ѥH�W�G�p�ߤ�{���A�o��![]() �A
�A![]() �C��Y����Ѭ�
�C��Y����Ѭ�
![]()
��P���T�ѧ����ۦP�C
��10-1.1 �t�m�k�P���Ǫ��k�ǽT�פ����
|
x |
���T�� |
N=1 |
N=2 |
||
|
�t�m�k* |
���Ǫ��k |
�t�m�k |
���Ǫ��k |
||
|
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 |
0.9168 0.8347 0.7545 0.6773 0.6042 0.5360 0.4738 0.4187 0.3715 |
0.908 0.822 0.742 0.668 0.600 0.538 0.482 0.432 0.388 |
0.908 0.822 0.742 0.668 0.600 0.538 0.482 0.432 0.388 |
0.9168 0.8347 0.7545 0.6773 0.6042 0.5360 0.4738 0.4187 0.3715 |
0.9168 0.8347 0.7545 0.6773 0.6042 0.5360 0.4738 0.4187 0.3715 |
�� �t�m�kN��1�ɡA�t�m�I���x��0.6�Q�Y�t�m�I���x��0.5�A�h���G���t�C
�ѥ��ҥi�o�{�U�ذt���ݭȪk����ܧ֦a��o�����D������ѡC���@��Ө����C��������ѡA�H���Ǫ��k����o���Ϊ����G�C��������ѫh�U��k�ұo���G���۷��ǽT�A���ѩ�t�m�k�u�ݸѤ@�եN���p�ߤ�{���A�Y�i�D�o�Y��![]() �A�Ө�L��k�h�������@�n���B�z�A�]���AN�ȸ��j�ɡA�t�m�k�̨�ϥμ�O�A�ӥB�{���]�p�]�̮e���C�]���A������l�U�`�N�ۭ���U�ؼƾǰt�m�k�����СC
�A�Ө�L��k�h�������@�n���B�z�A�]���AN�ȸ��j�ɡA�t�m�k�̨�ϥμ�O�A�ӥB�{���]�p�]�̮e���C�]���A������l�U�`�N�ۭ���U�ؼƾǰt�m�k�����СC
�ĤG�` �t���ݭȪk������
���F�����t���ݭȪk���ϥΤ�k�A�䦸�A�H��W��IJ�C�ɤl���|�V��Ǻ��z�ε���n���D�i�f�����Ҧ����ҡA�����t���ݭȪk�����Τ�k�C
![]() (10-2.1)
(10-2.1)
BC1 x��0�ɡA ![]() ��0
��0
BC2 x��1�ɡA y��1
�䤤y��C��Cs���L�]���@�סAx��r��R���L�]���b�|�A![]() �٬��Ʋ���(Thiele modulus)�CIJ�C�ɤl�����īY�Ƭ�
�٬��Ʋ���(Thiele modulus)�CIJ�C�ɤl�����īY�Ƭ�
![]() (10-2.2)
(10-2.2)
[A] �̧C���t���ݭȪky1(x)
��n=1�ɡA�Ҽ{���������ɱ���Y��{��(10-2.1)���̧C�������Ƭ�y1(x)=1+a1(1-x2)�A�N�J��{��(10-2.1)�o��ݭȪ��ܦ���
![]() (10-2.3)
(10-2.3)
�ھڰt���ݭȪk���w�q
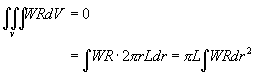
�� ![]() (10-2.4)
(10-2.4)
�t�m�k�G�t����Ƭ�![]() �F�Ox1=1/2�A�N�J��{��(10-2.4)�o��
�F�Ox1=1/2�A�N�J��{��(10-2.4)�o��![]() �A�G�o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
�A�G�o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
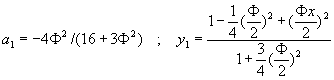 (10-2.5)
(10-2.5)
IJ�C�ɤl�����īY�Ƭ�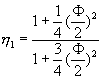 �C
�C
���Ǫ��k�G�t����Ƭ�![]() �A��
�A��![]() �F�N�J��{��(10-2.4)�o��
�F�N�J��{��(10-2.4)�o��![]() �A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
�A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
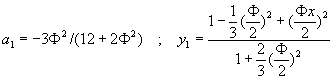 (10-2.6)
(10-2.6)
IJ�C�ɤl�����īY�Ƭ�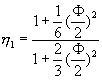 �C
�C
�ư϶��k�G�t����Ƭ�![]() �F
�F![]() �C�N�J��{��(10-2.4)�o��
�C�N�J��{��(10-2.4)�o��![]() �A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
�A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
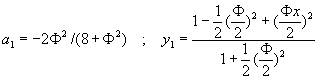 (10-2.7)
(10-2.7)
IJ�C�ɤl�����īY�Ƭ�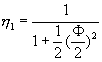 �C
�C
�D�q�k�G�t����Ƭ�![]() �F�N�J��{��(10-2.4)�o��
�F�N�J��{��(10-2.4)�o��![]() �A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
�A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
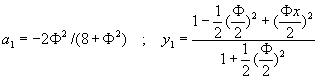 (10-2.8)
(10-2.8)
IJ�C�ɤl�����īY�Ƭ�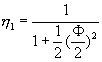 �C
�C
�̤p����k�G�t����Ƭ��ݭȹ良�w�Y�Ƥ��L���A![]() �A��
�A��![]() �F�N�t����ƥN�J��{��(10-2.4)�o��
�F�N�t����ƥN�J��{��(10-2.4)�o��![]() �A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
�A�n����o�쥼�w�Y��a1�ȤΤ@��������y1(x)��
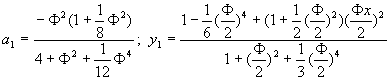 (10-2.9)
(10-2.9)
IJ�C�ɤl�����īY�Ƭ�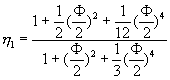 �C
�C
��k���: ��![]() �ɡA����U�ؤ�k�ұo���G�A�p��10-2.1�ҥܡC�i�H�o�{���Ǫ��k���G�̨ΡC
�ɡA����U�ؤ�k�ұo���G�A�p��10-2.1�ҥܡC�i�H�o�{���Ǫ��k���G�̨ΡC
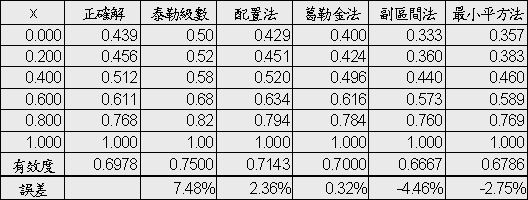
��10-2.1 �@���t���ݭȪk�ұo���G�����
[B] �����t���ݭȪkyN(x)
��n=1�ɡA�Ҽ{���������ɱ���Τ�{��(10-2.1)��N�������Ƭ�![]() �A�䤤
�A�䤤![]() �������L����{����ɱ���ơA
�������L����{����ɱ���ơA![]() �������L����{��������ɱ���(homogeneous boundary conditions)����ơC�N��{��(10-2.1)�Ө��A
�������L����{��������ɱ���(homogeneous boundary conditions)����ơC�N��{��(10-2.1)�Ө��A
![]() (10-2.10)
(10-2.10)
�αNN�������Ƽg���U���A�䤤�O![]()
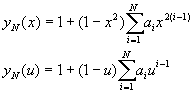 (10-2.11)
(10-2.11)
��{��(10-2.1)�i�H��g��
 (10-2.12)
(10-2.12)
�N��{��(10-2.11)�N�J��{��(10-2.12)�A�g��z��A�o��
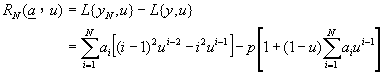 (10-2.13)
(10-2.13)
�ھڰt���ݭȪk���w�q
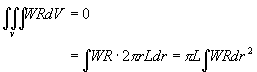
�Y ![]() �ΦA�g��u����Ƭ�
�ΦA�g��u����Ƭ�
![]() �Aj=1,2,�K,N (10-2.14)
�Aj=1,2,�K,N (10-2.14)
�N��{��(10-2.13)�N�J��{��(10-2.14)�A�n�����G�i�H�g���H�U���x�}���A
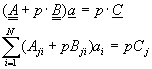 (10-2.15)
(10-2.15)
�䤤�x�}A�AB�A��C���O�]�t�����Wj(u)���w�q�ӷ|�����ܡC�Ѥ�{��(10-2.15)�o�쥼�w�Y�ư}�C��
![]() (10-2.16)
(10-2.16)
�N�����G�N�J��{��(10-2.11)�A�Y�i�o��L����{��������ѡC�P�ɡA�]�i�H�D�oIJ�C�����īY�Ƭ�
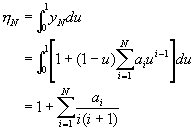 (10-2.17)
(10-2.17)
�t�m�k�G�t����Ƭ�![]() �F�N�J��{��(10-2.13)�Τ�{��(10-2.14)�A�o��
�F�N�J��{��(10-2.13)��{��(10-2.14)�A�o��
![]()
��
![]()
�P��{��(10-2.15)����A�o��x�}A�AB�A��C���O��
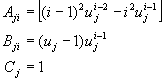 (10-2.18)
(10-2.18)
�Y�Ҽ{�ϥε����Z�t�m�I�A�ѩ�u0=0�AuN+1=1�A�h![]() �A�N�^��{��(10-2.17)�A�o��
�A�N�^��{��(10-2.17)�A�o��
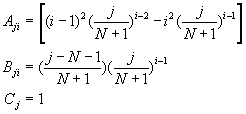 (10-2.19)
(10-2.19)
���Ǫ��k�G�t����Ƭ�![]() �F�N�J��{��(10-2.13)�Τ�{��(10-2.14)�A�o��
�F�N�J��{��(10-2.13)��{��(10-2.14)�A�o��![]() �A�n���i�}��A�o��x�}A�AB�A��C���O��
�A�n���i�}��A�o��x�}A�AB�A��C���O��
![]()
![]() (10-2.20)
(10-2.20)
![]()
�ư϶��k�G�t����Ƭ�![]() �F��L�϶�
�F��L�϶�![]() �C�N�J��{��(10-2.14)�A�o��
�C�N�J��{��(10-2.14)�A�o��![]() �C�N��{��(10-2.13)�N�J�A�n����o��o��x�}A�AB�A��C���O��
�C�N��{��(10-2.13)�N�J�A�n����o��o��x�}A�AB�A��C���O��
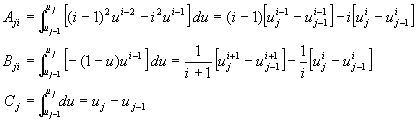 (10-2.21)
(10-2.21)
�Y�Ҽ{�ϥε����Z�϶��A�ѩ�u0=0�AuN+1=1�A�h![]() �C
�C
�D�q�k�G�t����Ƭ�![]() �F�N�J��{��(10-2.13)�Τ�{��(10-2.14)�A�o��
�F�N�J��{��(10-2.13)��{��(10-2.14)�A�o��
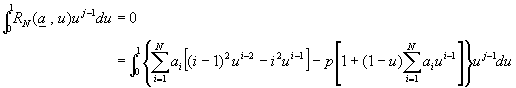
�n����o��x�}A�AB�A��C���O��
![]() (10-2.22)
(10-2.22)
![]()
![]()
�̤p����k�G�t����Ƭ��ݭȹ良�w�Y�Ƥ��L���A![]() �A��
�A��![]() �F�N���t����ƥN�J��{��(10-2.14)�A�ñN��{��(10-2.13)�N�J�A�n����i�H�o��x�}A�AB�A��C�C�ѩ�n�������A�����C�X�C
�F�N���t����ƥN�J��{��(10-2.14)�A�ñN��{��(10-2.13)�N�J�A�n����i�H�o��x�}A�AB�A��C�C�ѩ�n�������A�����C�X�C
�p���k�P�ϥε���
�t���ݭȪk���p���k�A�i�H�k�Ǧp�U:
(1) �Q�Τ@�Ӧh����![]() �@���L����{��L{y,u}��0������ѡF
�@���L����{��L{y,u}��0������ѡF
(2) �N�J�L����{��L{y,u}��0�A�D�X�ݭȪ����ܦ�R��L{yN,u
}-L{y,u}�Q
(3) ��ܨϥΪ��t���ݭȪk�A�w�q�t�����![]() �F
�F
(4) �ϴݭȪ��t���n���Ȭ��s
![]()
(5) �إ�N�ӥ��w�Y�ư}�Ca���p�ߤ�{���F
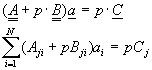
(6) �Q�μƭȤ�k���p�ߤ�{���A��X����h���������w�Y�ư}�Ca�Q
(7) �N�^�����h����![]() �A�إ߷L����{��������ѡQ
�A�إ߷L����{��������ѡQ
(8) �Q�ξA�������k�A�p��L����{���b�S�w��m���ѡC
�H�W�ҭz���p����p��10-2.12�ҥܡF�Q��Excel�ΰ������h�k�A���i�H�ܻ����a�إߩһݪ��{���C�Q��Excel�ҫإߵ{���p��10-2.2�ҥܡC�{���s�g�Ӹ`�i�Ѧҥ��ѩҪ����СC

��10-2.1 �t���ݭȪk�����


��10-2.2 (a) �Q��Excel�s�g�t���ݭȪk���d�ҡA�t�m�k�C�N�L����{�����D�ѡA�ܦ�²�檺�x�}�B��C�Q��Excel�Y�i�����a�������ȡAN=3�ұo���G�P���T�Ѭ۷��@�P�C

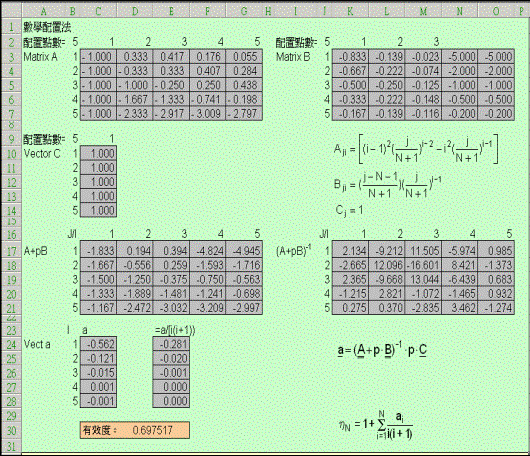
��10-2.2 (b)
�Q��Excel�s�g�t���ݭȪk���d�ҡA�t�m�k�C
N=5�ұo���G�C
�ĤT�` �ƾǰt�m�k
�W�@�`���A�ڭ̧Q��²�檺�u�ʰ��D���ҡA�����F�U��MWR�t���ݭȪk�Ψ�S�ʡA���`���h�N�w��t�m�k�@���Ժɪ��Q�סC�ϥΰt�m�k���ɭԡA�����Ƥΰt�m�I����ܤ�k�j�P�i�����T���G
(i) �����t�m�k(Interior Collocation)
�ҿ�Ϊ������ƺ�����ɱ���A�t�m�I��ܦ��L����{���ҦҼ{���϶����A�H�M�w���w�Y�ơC
(ii) ��ɰt�m�k(Boundary Collocation)
�ҿ�Ϊ������ƺ�����L����{���A�Ӱt�m�I�h�b��ɤW����A�H�M�w���w�Y�ơC
(iii) �V�M�t�m�k(Mixed Collocation)
�ҿ�Ϊ������Ƭ����N��ơA�䥼�w�Y�ƥѩҦҼ{�϶�������ɤW��w���t�m�I�ӨM�w�C
�t�m�k�`������ɭȱ`�L����{���B�S�x�Ȱ��D(Eigenvalue Problem)�ΰ��L�����D�ѡC�H�U�A�Q�δX�Ө��D�[�H�����C
��10-2
�@�������Ǿ�(K�ڱ`��)
�@���O�p��L�A�ⰼ�ūפ��O��T0��T1�C���q���Ť�{����
![]() �Q0��x��L (10-3.1)
�Q0��x��L (10-3.1)
BC1. T(0)��T0
BC2. T(L)��T1
�����O�����Ǿɲv�P�ū����Y��k(T)��k0�ϣ\(T��T0)�A�ըD��ūפ����C
[��] �O�L�]���ūפεL�]�����פ��O��
![]()
�h��L����{���i�H��g��
![]() �Q0�գi��1 (10-3.2)
�Q0�գi��1 (10-3.2)
�c(0)��1
�c(1)��1
�䤤a�ף\(T��T0)��k0�Q���F²�ƻ����_���A�Oa��1�A�h������ɱ���¦��ơA�i�H�g��
![]() (10-3.3)
(10-3.3)
�Y��N��2�A��ݭȬ�
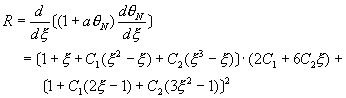 (10-3.4)
(10-3.4)
�t�m�I����![]() ��
��![]() �A�N�J�ݭȪ��ܦ��A�����ݭȦb�t�m�I�W��0�A�h�o
�A�N�J�ݭȪ��ܦ��A�����ݭȦb�t�m�I�W��0�A�h�o
C1�ס�0.5992
C2��0.1916
�G�o�c���G������Ѭ� ![]()
�ηūפ�������Ѭ�
![]()
��10-3
�D�u�ʷL����{��
�էQ�μƾǰt�m�k�ѫD�u�ʷL����{���C
![]() �Q0�գc��1 (10-3.5)
�Q0�գc��1 (10-3.5)
BC1 �c(0)��0
BC2 �c(1)��0
[��] ������ɱ���¦��ƥi��
![]() (10-3.6)
(10-3.6)
�Ҽ{��²�檺���p�AN��1�A�Y![]() �C�h�ݭȬ�
�C�h�ݭȬ�
![]() (10-3.7)
(10-3.7)
���t�m�I��x��0.5�Q�OR�b�t�m�I�W��0�A�o��
![]()
�Q�Τ��y�k�D�o�W�����Ѭ�C1��0.44712�C�G�c1��
![]()
�P���T�Ѥ�����p�U���A���G��ܥγ�²�檺����ѡA�ĪG�٤����O�I
|
x |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|
���T�� |
-0.0414 |
-0.0733 |
-0.0958 |
-0.1092 |
-0.1137 |
|
�c1 |
-0.0402 |
-0.0715 |
-0.0939 |
-0.1073 |
-0.1178 |
|
�~�t% |
2.8 |
2.4 |
1.99 |
1.73 |
1.69 |
�ĥ|�` ����t�m�k
�t�m�k�ϥΤ�K�A����ǽT�o�M�w���¦��ƪ���ܡBN�Ȫ��j�p�ΰt�m�I����ܡC1938�~���Y��(Lanczos)��ij�Q�Υ���ż�(Orthogonal Polynomials)�@����¦��ơA�åH����żƪ��ڧ@���t�m�I�Q��ӦA�g�L�Q�w�ˤΥv����(Villadsen and Stewart)����i�A�ثe�w�����Q�ϥαo�̼s�x���t�m�k�A�q�٬��u����t�m�k�v(Orthogonal Collocation Method)�C
����t�m�k�W�O�H����żƧ@����¦��ơQ�p�G��¦��ƪ��̰����Ƭ�N�A�h�Q��N��1��������żƪ��ڧ@���t�m�I�C�ѩ�żƨ㦳�\�h����B�z���ƾǯS�ʡA�]���A����t�m�k��z���P�e�z�t�m�k�����@�P�A���ϥΤW�o�i���Υ���żƪ��S�ʡA�ϳB�z��k��²�ơA��A��Q�έp����ӨD�ѡC
���]�@�L����{��������ѡA�i�H�Q�Τ@�ե���ż�P(x)���u�ʩM�Ӫ��ܡA
![]() (10-4.1)
(10-4.1)
�b�H�W����{�����`�@��N��2�ӥ��w�Y��![]() �A�������yN���U���Хu�g��N�A�O�ѩ���ɭȱ`�L����{��(BVP ODE)�������ɱ���w�g�i�H�M�w���
�A�������yN���U���Хu�g��N�A�O�ѩ���ɭȱ`�L����{��(BVP ODE)�������ɱ���w�g�i�H�M�w���![]() �ȡA�u�ݭn�A�Q��N�Ӥ����t�m�I�Y�i�H�M�w�Ҧ�
�ȡA�u�ݭn�A�Q��N�Ӥ����t�m�I�Y�i�H�M�w�Ҧ�![]() �ȡA�G�g��yN�F�䤤�AN�N���һݪ������t�m�I�ơC
�ȡA�G�g��yN�F�䤤�AN�N���һݪ������t�m�I�ơC
����ż�P(x)�i�H�g���żƪ��@����ܦ�
![]() (10-4.2)
(10-4.2)
�䥿��ʽ謰
![]() �Qk��0�A1�A2�A�K�K�Am��1 (10-4.3)
�Qk��0�A1�A2�A�K�K�Am��1 (10-4.3)
�䤤(a�Ab)����ɭȱ`�L����{�����w�q�d��A�q�`�����Q�ήy���ܴ��ಾ��(0�A1)�A�H�K�B�z�C
�N��{��(10-4.2)�N�J��{��(10-4.1)���A�i�N��¦���yN��g���H�U���覡�A�H�Q�p��B�z�G
![]() (10-4.4)
(10-4.4)
���]�i�H�Q�ξA����k�o��t�m�I�A�h�b�t�m�Ixj��m�W����ƭ�yN��
![]() �Qj��1�A2�A�K�K�AN��2 (10-4.5)
�Qj��1�A2�A�K�K�AN��2 (10-4.5)
x1��0�A xN��2��1
�Ӧb�t�m�Ixj��m�W�AyN���@���ΤG���ɨ�ơA��i���O�Ѥ�{��(10-4.4)��x�@�L���A�o��
![]() (10-4.6)
(10-4.6)
![]() (10-4.7)
(10-4.7)
�O�x�}![]() �A
�A![]() ��
��![]() ���O��
���O��
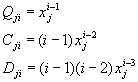 (10-4.8)
(10-4.8)
�O�}�C![]() �A
�A![]() �A�h��{��(10-4.5)�A(10-4.6)��(10-4.7)���O��g���x�}�Ÿ���A�o��
�A�h��{��(10-4.5)�A(10-4.6)��(10-4.7)���O��g���x�}�Ÿ���A�o��
![]() (10-4.9)
(10-4.9)
![]() (10-4.10)
(10-4.10)
![]() (10-4.11)
(10-4.11)
�ھڤ�{��(10-4.8)�i���A�Y�w���t�m�I��m�A�h�x�}![]() �A
�A![]() ��
��![]() ���i�H�ܧ֪��p��X�ӡC�ӥѤ�{��(10-4.9)�A�i�H�N���w�q���Y�ư}�C
���i�H�ܧ֪��p��X�ӡC�ӥѤ�{��(10-4.9)�A�i�H�N���w�q���Y�ư}�C![]() ���ܦ��t�m�I�W����ƭ�
���ܦ��t�m�I�W����ƭ�![]() �����Y
�����Y
![]() (10-4.12)
(10-4.12)
�N�W���N�^��{��(10-4.10)��{��(10-4.11)���A�i�H���O�o��
![]() (10-4.13)
(10-4.13)
![]() (10-4.14)
(10-4.14)
�ھڤ�{��(10-4.8)�i���A�Y��w�@�հt�m�I![]() �A�h
�A�h![]() �B
�B![]() ��
��![]() ���i�����D�o�A�ӤW�G��{����
���i�����D�o�A�ӤW�G��{����![]() �B
�B![]() �]���i�H�Q�ίx�}�ާ@�ܧ֪��D�o�C�]���A�i�N�L����{�������@���ΤG���ɨ�ƶ��A�����ܦ��t�m�I��m����ƭ�
�]���i�H�Q�ίx�}�ާ@�ܧ֪��D�o�C�]���A�i�N�L����{�������@���ΤG���ɨ�ƶ��A�����ܦ��t�m�I��m����ƭ�![]() ���u�ʨ�ơA�ӱN��L����{����Ʀ��@���p�ߥN�Ƥ�{���C�x�}A��B�Y�٬��L���ާ@�x�}�C�Q�ηL���ާ@�x�}�A�i�H�N�L����{����g����ƭ�
���u�ʨ�ơA�ӱN��L����{����Ʀ��@���p�ߥN�Ƥ�{���C�x�}A��B�Y�٬��L���ާ@�x�}�C�Q�ηL���ާ@�x�}�A�i�H�N�L����{����g����ƭ�![]() ���u�ʨ�ơA��Y�ܦ��@�սu���p�ߤ�{���C�Q�ΰ������h�k�ξA���ƭȤ�k�A�Y�i�D�o�b�t�m�I�B����ƭ�
���u�ʨ�ơA��Y�ܦ��@�սu���p�ߤ�{���C�Q�ΰ������h�k�ξA���ƭȤ�k�A�Y�i�D�o�b�t�m�I�B����ƭ�![]() �C
�C
�H�W�һ���������t�m�k����A�i�H�k�Ǧp�U�G
(1)
�Q�Υ���h�������ѡA�o��@�հt�m�I![]() �F
�F
(2)
�Q�Τ�{��(10-4.8)�ΰt�m�I![]() �A�إ߯x�}
�A�إ߯x�}![]() �A
�A![]() ��
��![]() �F
�F
(3)
�إߤ@���L���ާ@�x�}![]() �A�䤤
�A�䤤![]() �F
�F
(4)
�إߤG���L���ާ@�x�}![]() �A�䤤
�A�䤤![]() �F
�F
(5)
�Q����ɱ���إ�y1��yN+2�����ܦ�(�b�����Ĥ��`���Բӻ���)�F
(6)
�N�L���ާ@�x�}�N�J��L����{���A�إߨ�ƭ�![]() ���p�ߤ�{���F
���p�ߤ�{���F
(7)
�Q�ΰ������h�k�Ψ�L�A���ƭȤ�k�A�D�Ѩ�ƭ�![]() ���p�ߤ�{���F
���p�ߤ�{���F
(8)
�Q�ξA�������k�A�إ߯S�w�I����ƭ�y�C
��10-4
�Q�ΰt�m�k����ɭȱ`�L����{��
![]()
BC1 y(0)��0
BC2 y(1)��1
[��] ���F�����_���A�ڭ̥u�Ҽ{��²�檺���pN��1�A�hN��2�Ӱt�m�I���O��![]() �A
�A![]() ��
��![]() �C�ھڤ�{��(10-4.8)�o
�C�ھڤ�{��(10-4.8)�o![]() �A
�A![]() ��
��![]() ���O��
���O��
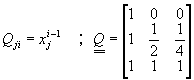
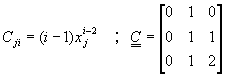

�x�}![]() ���ϯx�}
���ϯx�}![]() �i�Q�ΰ��������k�D�o��
�i�Q��������k�D�o��
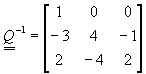
�]���A�L���ާ@�x�}�i���O�ھڨ�w�q�D�o�C
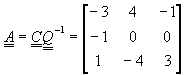
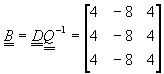
�N�^��L����{���o��
![]() �@�Qj��1�A2�A�K�K�AN��2
�@�Qj��1�A2�A�K�K�AN��2
�ѩ�y1��0�AyN��2��y3��1�A�u�ѤUy2�����A�]���A�u�Ҽ{N��1�Bj��2�����p�A�ѤW���o
![]()
�Ny1��y3�N�J�A�o![]() �A�ѻPy2��0�A�]���A�i�H�o��y2��0.57916�C
�A�ѻPy2��0�A�]���A�i�H�o��y2��0.57916�C
�Q�γo�سB�z�覡�A�ڭ̥i��o�U�t�m�I��m��y�ȡC�Y�ݨ�L��m��y�ȡA�h�i�Q�Υ��ѲĤT���Ҥ��Ъ����Ȫk�D���C�ݭn�Dy���n���ȡA�h�i�Q�Υ��ѲĤ����Ҥ��Ъ������n���k(Gauss Quadrature)�D���C
�Ĥ��` ����t�m�k��ɱ��B�z
�L����{������ɱ���q�`�i�����T�j���A���`�N�H��Ҩӻ����ϥΥ���t�m�k�ɡA��ɱ��B�z��k�C
�Ҽ{�@�`�L����{������
![]() (10-5.1)
(10-5.1)
�䥿�T�Ѭ�
![]() (10-5.2)
(10-5.2)
�Q�ΤW�@�`�Ҥ��Ъ��B�z��k�A��{��(10-5.1)�i�H�Q��g��
![]() �Qj��1�A2�A�K�K�AN+1 (10-5.3)
�Qj��1�A2�A�K�K�AN+1 (10-5.3)
�αNy1��yN+1�����{���k���A��g��
![]()
(10-5.4)
�䤤�_ji�٬�Kronecker Delta�A�w�q��
![]() (10-5.5)
(10-5.5)
��{��(10-5.4)���Ay1��yN��2�q�`�Q����ɱ���M�w���A�H�U���O�Q�ΦU�ؤ��P����ɱ���[�H�����C
[A] ��ɱ���(I �w I)
�ⰼ��ɱ����Ĥ@��(Dirichlet)��ɱ���G
BC1 y(0)��0�Q x��0
BC2 y(1)��1�Q x��1 (10-5.6)
�W���i��g��y1��0�AyN��2��1�A�N�J��{��(10-5.4)�o��
![]()
�ΧQ�ίx�}�Ÿ�²�g��
![]()
�ζi�@�B²�ơA�üg���H�U���x�}��{��
![]() (10-5.7)
(10-5.7)
�䤤
![]()
��{��(10-5.7)�N���@�սu���p�ߤ�{���A�i�Q�ΰ������h�k�Ѥ��C
[B] ��ɱ���(I �w II)
���I����ɱ��Ĥ@����ɱ���A�bx=1��m����ɱ��ĤG����ɱ���G
BC1 y(0)��0�Q x��0
BC2 ![]() �Q x��1 (10-5.8)
�Q x��1 (10-5.8)
�Y�Hyi���ܡA�h�o��
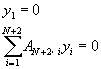
�ѤW���D�oyN��2��
![]()
�N�^��{��(10-5.4)�A�o��
![]()
j��2�A3�A�K�K�AN��1
�μg��
![]() (10-5.9)
(10-5.9)
�䤤
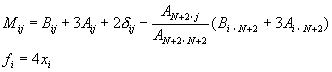
[C] ��ɱ���(I �w III)
���I����ɱ��Ĥ@����ɱ���A�bx=1��m����ɱ��ĤT����ɱ���G
BC1 y(0)��0�Q x��0
BC2 ![]() �Q x��1 (10-5.10)
�Q x��1 (10-5.10)
BC2�i�Q�Τ@���ɨ�ƾާ@�x�}���ܬ�
![]()
��z���A�çQ��BC1(y1��0)�C�i�H�o��
![]()
�N�J��{��(10-5.4)�o��
![]()
�ΥH�x�}�Ÿ����ܬ�
![]() (10-5.11)
(10-5.11)
�䤤
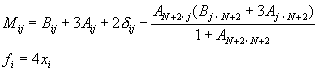
[D] ��ɱ���(II �w I)
���I����ɱ��ĤG����ɱ���A�bx=1��m����ɱ��Ĥ@����ɱ���G
BC1 ![]() �Q x��0
�Q x��0
BC2 y��1�Q x��1 (10-5.12)
��H�W�B�z�A�o��
![]()
��
![]() (10-5.13)
(10-5.13)
![]()
![]()
[E] ��ɱ���(II �w II)
�ⰼ��ɱ����ĤG����ɱ���G
BC1 ![]() �Q x��0
�Q x��0
BC2 ![]() �Q x��1 (10-5.14)
�Q x��1 (10-5.14)
��H�W�B�z�A�oy1��yN��2���O��
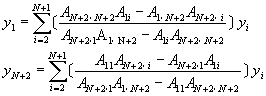
�αN�W�����A���������ܦ��H![]() ���ܡA�üg��
���ܡA�üg��
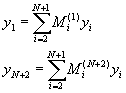
�N�J��{��(10-5.4)�o��
![]() (10-5.15)
(10-5.15)

[F] ��ɱ���(II �w III)
���I����ɱ��ĤG����ɱ���A�bx=1��m����ɱ��ĤT����ɱ���G
BC1 ![]() �Q x��0
�Q x��0
BC2 ![]() �Q x��1 (10-5.16)
�Q x��1 (10-5.16)
BC1��BC2���O�i�ηL���ާ@�x�}�g���G
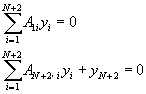
�ξ�z��
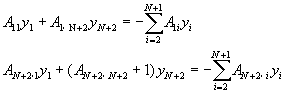
�ѥH�W�p�ߤ�{���A�oy1��yN��2���O��
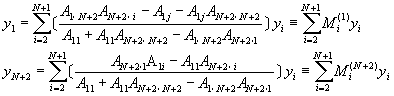
�N�W���N�J��{��(10-5.4)�o��
![]() (10-5.17)
(10-5.17)
�䤤
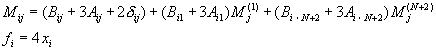
[G] ��ɱ���(III �w III)
�ⰼ��ɱ����ĤT����ɱ���G
BC1 ![]() �Q x��0
�Q x��0
BC2 ![]() �Q x��1 (10-5.18)
�Q x��1 (10-5.18)
�Q�ηL���ާ@�x�}![]() �A�Y
�A�Y![]() �A�i�N��ɱ����g��
�A�i�N��ɱ����g��
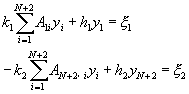
��z��y1��yN��2���p�߽u�ʤ�{����
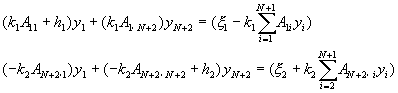
�ѥH�W�G��{���A�i�p�߸ѱoy1��yN��2���O��
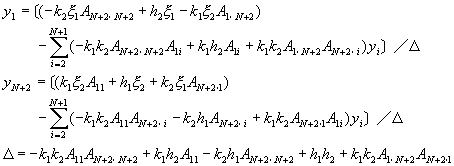
�ΥH�Ÿ��N���A²�g��
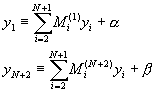
�N�W���N�J��{��(10-5.4)�A�i�H�o��
![]() (10-5.19)
(10-5.19)
�䤤
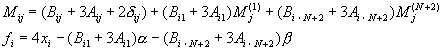
�H�W�Y�ھڱ`�L����{��![]() ���ҡA�Ұ����t�ɻP�����AŪ�̰w��S�w�L����{���D�ѮɡA�i�ھڬۦP�@�k�@�A���B�z�C
���ҡA�Ұ����t�ɻP�����AŪ�̰w��S�w�L����{���D�ѮɡA�i�ھڬۦP�@�k�@�A���B�z�C
�Ĥ��` ���i���h�����P�ާ@�x�}
����t�m�k�Y�ĥΥ���h�����@����¦��ơA�Q�Υ���h�������S�ʡA²�Ƽƾǰt�m�k���B�z�{�ǡC�`�Ϊ�����h�����]�A���ڼw�h����(Legendre Polynomial)�Υ��`�Ҥ��Ъ����i���h����(Jacobi Polynomial)���C�H�U�w�ﶮ�i���h�������S�ʤΦp��Q�Ψ�S�ʼ��g�{���A�@²�n�����C
[��] ���i���h�������w�q
���i���h�����O�@�ب嫬������h�����A��w�q��
![]() �Qj��0�A1�A2�A�K�K�AN��1 (10-6.1)
�Qj��0�A1�A2�A�K�K�AN��1 (10-6.1)
�Ϊ��ܦ�
![]() (10-6.2)
(10-6.2)
![]()
�������i���h�������Բӻ����A�аѦҤu�{�ƾǮ��y�C
[��] ���i���h������ù�wͺ����ܪk
�Hù�wͺ���{��(Rodrigues�� Formula)���ܡA���i���h�����i�H�g��
![]() (10-6.3)
(10-6.3)
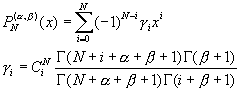
[C] ���i���h�������`�ǭp�⤽�����ܪk
���i���h�������`�ǭp�⤽��(Recurrence formula)��
pN = [x - gN(N,a,b)] pN-1
�V hN(N,a,b) pN-2 ;
p0 = 0 (10-6.4)
![]()
![]() ;
; ![]()
h1 = 0 ; ![]()
![]()
[D] �`�������i���h����
�`�������i���h�����p�U���ҥܡG
|
a |
b |
N=0 |
N=1 |
N=2 |
N=3 |
|
0 |
0 |
1 |
2x-1 |
6x2-6x+1 |
20x3-30x2+12x-1 |
|
1 |
0 |
1 |
3x-1 |
10x2-8x+1 |
35x3-45x2+15x-1 |
|
2 |
0 |
1 |
4x-1 |
15x2-10x+1 |
56x3-63x2+18x-1 |
|
0 |
1 |
1 |
|
|
|
|
1 |
1 |
1 |
2x-1 |
6x2-6x+1 |
14x3-21x2+9x-1 |
|
2 |
1 |
1 |
|
|
|
��10-5
���i���h�������p��
�ըD![]() ���ȡC
���ȡC
[��]
gN=1/2
![]()
![]()
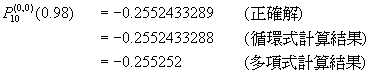
�Ѷ��i���h�������`�ǭp�⤽��(Recurrence formula)pN = [x - gN(N,a,b)] pN-1
�V hN(N,a,b) pN-2 �A
p0 = 0�Q�Q�Τ��y�k�D���i���h�������ڧ@���t�m�Ixi�ɡA���]�w�g���Dx1�Bx2�B�K�Bxk�@k�ӸѡA�n�D��k+1�ӸѮɡA�i�H�Q�λ��U���![]() �A�N�w������x1�Bx2�B�K�Bxk�Ѧh����������h�����C�A�Q�Τ��y�k�ѻ��U���GN-K�A�o�쭡�N����
�A�N�w������x1�Bx2�B�K�Bxk�Ѧh����������h�����C�A�Q�Τ��y�k�ѻ��U���GN-K�A�o�쭡�N����
xk+1,i= xk+1,i-1 �V
d(x) (10-6.5)
�䤤
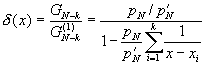
![]()
![]()
����ɡA�Oxk+1,0 �����j�� xk ���Ʀr�A�Yxk+1,0 = xk + e�Q�䤤e���@�ӫܤp���ȡA�Ҧp10-4�C���i���h�����Q�Υ��` [C] ����{���p��A��p��D�oxk+1��A��k�W�[1�A�A���ƥH�W�B�J�C�Q�γo�ؤ�k�ҫإߪ��Ƶ{���p�U�ҥܡC
|
'
========================== '
ROOTS OF JACOBI POLYNOMIAL '
========================== �� Diff1(I) = G(I)
�� Diff2(I) = H(I) �� AlphaPlusBeta
= Alpha + Beta AlphaMinusBeta
= Beta - Alpha AlphaBeta
= Beta * Alpha Diff1(1)
= (AlphaMinusBeta / (AlphaPlusBeta + 2) + 1) / 2 Diff2(1)
= 0 ��
Calculate G(I) & H(I) If
N >= 2 Then For I = 2 To N
IM1 = I - 1 Z
= AlphaPlusBeta + 2 * IM1 Diff1(I)
= (AlphaPlusBeta * AlphaMinusBeta / Z / (Z + 2) + 1) / 2
If I = 2 Then
Diff2(I) = (AlphaPlusBeta + AlphaBeta + IM1) / Z / Z / (Z + 1)
Else
Z = Z * Z
Y = IM1 * (AlphaPlusBeta + IM1)
Y = Y * (AlphaBeta + Y)
Diff2(I) = Y / Z / (Z - 1)
End If Next I End
If '
Newton��s Method to find ROOT X
= 0 For
I = 1 To N Do
XD = 0
XN = 1
XE = 0
XM = 0
For J = 1 To N
XP = (Diff1(J) - X) * XN - Diff2(J) * XD
XQ = (Diff1(J) - X) * XM - Diff2(J) * XE - XN
XD = XN
XE = XM
XN = XP
XM = XQ
Next J
ZC = 1 Z
= XN / XM
If I > 1 Then
For J = 2 To I
ZC = ZC - Z / (X - Root(J - 1))
Next J
End If Z
= Z / ZC X
= X - Z Loop While (Abs(Z) >
0.000000001) Root(I) = X X = X + 0.0001 Next
I ��
To include ROOT at x= 0 and x=1 If
(N1 = 1) Then For I = 1 To N J
= N + 1 - I
Root(J + 1) = Root(J) Next I Root(1) = 0 End
If If
(N2 = 1) Then Root(ND) = 1 ��
Print ROOTs for the Polynomial Print Print
"** COLLOCATION POINTS:" Print For
I = 1 To ND Print Format(Root(I),
" 0.000000E+00 ") Next
I |
[F] ���i���h�������ɨ��
���]�Q�� [E] ���Ҥ��Ъ����y�k�A�i�H�o�춮�i���h������N+1�ӮڡAxj�Aj=1,2,�K.,N+1�A�h�i�N���i���h�����g��
![]() (10-6.6)
(10-6.6)
�Χ�g���`�ǭp�⦡
p0(x)
= 1
pj(x)
= (x-xj) pj-1(x) �Q j = 1, 2, �K�K, N+1 (10-6.7)
�N�W���L���A�i�H�o��
![]() (10-6.8)
(10-6.8)
![]() (10-6.9)
(10-6.9)
![]() (10-6.10)
(10-6.10)
�ѩ�![]() �A�]���A�Q�ΥH�W��{���A�i�H�ܧ֪��D�o�b�U�t�m�I��m�W���ɨ�ƭȡC�g���Ƶ{���d�Ҧp�U�C
�A�]���A�Q�ΥH�W��{���A�i�H�ܧ֪��D�o�b�U�t�m�I��m�W���ɨ�ƭȡC�g���Ƶ{���d�Ҧp�U�C
|
��
Prepare Derivatives of the Polynomial For
I = 1 To ND X = Root(I) Diff1(I) = 1 Diff2(I) = 0 Diff3(I) = 0 For J = 1 To ND
If J <> I Then
Y = X - Root(J)
Diff3(I) = Y * Diff3(I) + 3 * Diff2(I)
Diff2(I) = Y * Diff2(I) + 2 * Diff1(I) Diff1(I) = Y *
Diff1(I)
End If Next J Next
I |
[G] ���i���h�����P�Ԯ����_�����k
�Ѧҥ��ѲĤT���ƭȤ����k�������A�Y�w��(xi�Ayi)�Ai=1,2,�K..,N+1�A�hyN(x)�i�H�Q�ΩԮ����_�����k(Lagrangian Interpolation)�g��
![]() (10-6.11)
(10-6.11)
�Q�γo�ؤ�k�ҫإߪ������k�Ƶ{���p�U�ҥܡC
|
'
======================== '
LAGRANGIAN INTERPOLATION '
======================== POL
= 1 For
I = 1 To ND YVA = X1 - Root(I) XP(I) = 0 If YVA = 0 Then XP(I) = 1 POL = POL * YVA Next
I If
POL <> 0 Then For I = 1 To ND XP(I)
= POL / Diff1(I) / (X1 - Root(I)) Next I End
If |
[H] ���i���h�����P�L���ާ@�x�}
�ھکԮ����_������{��(10-6.11)�A���L���A�i�H�o��y(x)���@���ΤG���ɨ�Ƥ��O��
![]() (10-6.12)
(10-6.12)
![]() (10-6.13)
(10-6.13)
�䤤
![]()
![]()
![]()
![]()
�䤤���i���h�������ɨ��![]() �i�H�Q�Τ�{��(10-6.8)�B(10-6.9)��(10-6.10)�D���C�Q�γo�ؤ�k�ҫإߪ��Ƶ{���p�U�ҥܡC
�i�H�Q�Τ�{��(10-6.8)�B(10-6.9)��(10-6.10)�D���C�Q�γo�ؤ�k�ҫإߪ��Ƶ{���p�U�ҥܡC
|
Sub
DefMatrix(ID, ND, N1, N2, Diff1, Diff2, Diff3, Root, Vect, A, B) '
============================= '
DERIVATIVE OPERATION MATRICES '
============================= For
I = 1 To ND ID = 1 Call OpMatrix(I, ID, ND,
N1, N2, Diff1, Diff2, Diff3, Root, Vect) For J = 1 To ND
A(I, J) = Vect(J) Next J ID = 2 Call OpMatrix(I, ID, ND, N1,
N2, Diff1, Diff2, Diff3, Root, Vect) For J = 1 To ND
B(I, J) = Vect(J) Next J Next
I End
Sub Sub
OpMatrix(I, ID, ND, N1, N2, Diff1, Diff2, Diff3, Root, Vect) '
================ '
OPERATION MATRIX '
================ '
--ENTRY POINT For J = 1 To ND
If J = Index Then
If ID = 1 Then
Vect(J) = Diff2(Index) / Diff1(Index) / 2
Else
Vect(J) = Diff3(Index) / Diff1(Index) / 3
End If
Else
Y = Root(Index) - Root(J)
Vect(J) = Diff1(Index) / Diff1(J) / Y
If ID = 2 Then Vect(J) = Vect(J) * (Diff2(Index) / Diff1(Index) - 2 /
Y)
End If Next J End Sub |
[I] ���i���h�����P�����ƭȿn��
�n���ާ@�i�H�ĥΥ��ѲĤ����Ҥ��Ф������n���k�C
![]() (10-6.14)
(10-6.14)
�䤤�A�D�X�n���t�����wi�A�Y�i�p��n�����G�C�������i���t����Ƭ�
W(x)
= xb(1-x)a
(10-6.15)
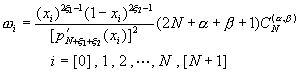 (10-6.16)
(10-6.16)
�Yx=�����n���t�m�I�A�hx1 = 1�A�_�hx1 = 0�C
�Yx=�����n���t�m�I�A�hx2 = 1�A�_�hx2 = 0�C
[J] �p�D�Pù�B�S�ƭȿn��
���F�����n���k�H�~�A�p�D�Pù�B�S(Radau and Lobatto)�n���k�]�O���`�Q�ϥΪ��ƭȿn����k�C��t����Ƭ�
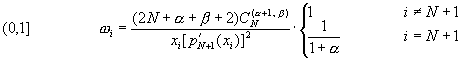
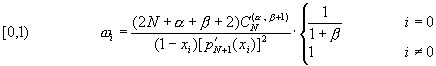
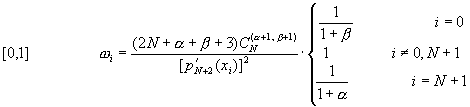
(10-6.17)
�䤤�Ĥ@�βĤG���٬��p�D�ƭȿn���t���A�ĤT���٬�ù�B�S�ƭȿn���t���C
�ĤC�` �u�ʰ��D���{���W��
�ھڥH�W�Ѹ`�����СA�ڭ̥i���w�X�Q�Υ���t�m�k�ѷL����{�����X���B�J�G
�]i�^
�ȤW�@�~�G
l
����ɱ����i�ɥXy1��yN��2�����ܦ�(�p�����Ĥ��`������)�C
l
�Q�ηL���ާ@�x�}![]() ��
��![]() �A�N�L����{���ഫ��
�A�N�L����{���ഫ��
![]()
�üg�U![]() ��
��![]() �����ܤ�k�C
�����ܤ�k�C
�]ii�^
�{���W���G
l
�M�w�ϥΪ�N��(�q�`���4��10���Y�i�o��۷����T����)�C
l
�M�w�ϥΪ�����żƺ����C
l
�]�p�{����X����h����PN(x)����xj�Aj��1�A2�A�K�K�AN�A�@���t�m�I�C
l
�]�p�{���D�X�L���ާ@�x�}![]() ��
��![]() �C
�C
l
�إ�![]() ��
��![]() �A�ñN�L����{����g���p�ߤ�{���C
�A�ñN�L����{����g���p�ߤ�{���C
l
�Q�ΰ������h�k�ѽu���p�ߤ�{��![]() �A�D�o�t�m�I�W����ƭ�
�A�D�o�t�m�I�W����ƭ�![]() �C
�C
l
�Q�Τ����k�H�A��x���Z�C�Ly�ȡC
�ĤK�` �D�u�ʱ`�L����{��
�D�u�ʱ`�L����{���W�����T�j���G(1)�u�ʱ`�L����{���A��ɱ���D�u�ʡQ(2)�D�u�ʱ`�L����{���A��ɱ��u�ʡQ(3)�D�u�ʱ`�L����{���A�D�u����ɱ���C����H�W�U�`�B�z��A�o�T���D�u�ʱ`�L����{�����i�ܦ��@���p�ߪ��D�u�ʥN�Ƥ�{���A�Q�Υ��ѩҤ��Ъ����y�Ժִ˪k�γνu�k�Y�i��H�W�U�`�D�o![]() �C�H�U�Q�ι�һ������C
�C�H�U�Q�ι�һ������C
�ѦҤ��m
1.
Finlayson, B. A., ��The Method of
Weighted Residuals and Variational Principles�� Academic Press, (1972).
2.
Villadsen, J., and M. L. Michelsen;
��Solution of Differential Equation Models by Polynomial Models��, Prentice-Hall,
(1978).
3.
Finalyson, B. A., ��Nonlinear Analysis
in Chemical Engineering��. (1980).
4.
Davis, M. E., ��Numerical Methods and
Modeling for Chemical Engineers��, John Wiley, New York, (1984).
5.
Aris, R. ��The Mathematical Theory of
Diffusion and Reaction in Permeable Catalysts��. Oxford, Clarendon Press (1975).
6.
Carberry, J. J., ��Chemical and
Catalytic Reaction Engineering�� McGraw-Hill, New York, (1976).
7.
Weisz, P. B., and J. S. Hicks, ��The
Behavior of Porous Catalyst Particles in View of Internal Mass and Heat
Diffusion Effects��, Chem. Eng. Sci., 17, 265 (1962).





