回首頁     回第三部

第十一章  偏微分方程式

工程科學是一門經常需要面對複雜現象，需要大量仰賴經驗及資料的科學，工程師或研究人員時常需面對複雜的自然現象，然後利用簡化的數學模式進行分析探討，以便進行設計或計算。

許多自然界的現象都可以利用偏微分方程式加以描述﹔典型的二階線性偏微分方程式，可以利用以下的一般式表示之:

                                                            (11-0.1)

其中x為自變數，y為因變數。

第一節  偏微分方程式的分類

線性二階偏微分方程式依係數Ai及Bi的特性，可分類為拋物線型偏微分方程式、橢圓型偏微分方程式及雙曲線型偏微分方程式三大類。詳見工程數學相關書籍。

拋物線型偏微分方程式: 偏微分方程式(11-0.1)中的二次導函數有一個係數Ak為零﹔其他Ai都不等於零，且正負符號都相同﹔且。例如﹔

                                                                                   (11-1.1)

橢圓型偏微分方程式: 偏微分方程式(11-0.1)中所有的二次導函數係數Ai都不等於零，且正負符號都相同。例如﹔

                                                                              (11-1.2)

雙曲線型偏微分方程式: 偏微分方程式(11-0.1)中所有的二次導函數係數Ai都不等於零，且其中一Ai正負符號與其他Aj不相同。例如﹔

                                                                                   (11-1.3)

第二節  有限差分近似法

本書第八章已經針對如何利用有限差分法處理常微分方程式的導函數作了詳細說明，各種導函數的差分近似方程式，在第八章中也作過詳細討論。對於偏微分方程式中的導函數之有限差分，可以利用完全相同的方式處理之。

假設偏微分方程式中的應變數u為自變數x及y的函數，或以函數關係表示為u=u(x,y)，則利用泰勒級數將u(x,y)展開，可以得到

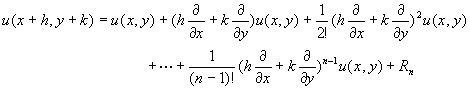 (11-2.1)

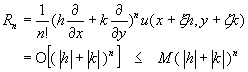                                                    (11-2.2)

當自變數x及y的差分增量h及k趨近於零時，n項泰勒級數展開的捨去誤差Rn值也會趨近於零，使方程式(11-2.1)的誤差變成小得可以接受。

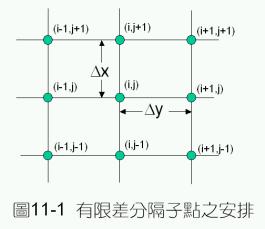
考慮如圖11-1所示之有限差分格子點，其中格子點可以簡稱為(i,j)，其周圍的格子點標示符號如圖11-1所示。

若針對格子點(i,j)鄰近的格子點ui-1,j+1、ui,j+1、ui+1,j+1、ui-1,j、ui+1,j、ui-1,j-1、ui,j-1、ui+1,j-1對中間格子點ui,j作泰勒級數開，則由方程式(11-2.1)的一般式，可以分別得到

                 (11-2.3)

                          (11-2.4)

                  (11-2.5)

                  (11-2.6)

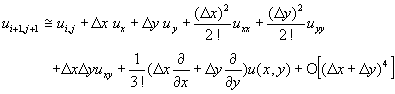         (11-2.7)

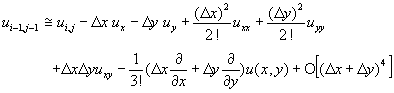         (11-2.8)

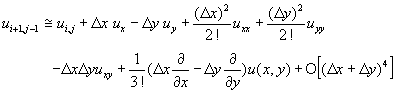         (11-2.9)

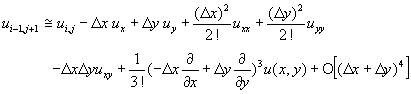      (11-2.10)

在以上的方程式中，，，餘此類推。且所有的導函數值需在格子點(i,j)位置計算。

向後差分

由方程式(11-2.3)及方程式(11-2.5)，可以得到一次導函數的向後差分(Backward Difference)表示式為

                                                                   (11-2.11)

                                                                    (11-2.12)

前進差分

由方程式(11-2.4)及方程式(11-2.6)，可以得到一次導函數的前進差分(Forward Difference)表示式為

                                                                   (11-2.13)

                                                                    (11-2.14)

中央差分

由方程式(11-2.3)及方程式(11-2.4)相減，可以得到一次導函數的中央差分(Central Difference)表示式為

                                                             (11-2.15)

同理由方程式(11-2.5)及方程式(11-2.6)相減，可以得到

                                                              (11-2.16)

又由方程式(11-2.3)及方程式(11-2.4)相加，可以得到二次導函數的中央差分(Central Difference)表示式為

                                                (11-2.17)

                                                 (11-2.18)

將方程式(11-2.7)加上方程式(11-2.8)，然後減去方程式(11-2.9)及方程式(11-2.10)，得到uxy的差分表示式為

                   (11-2.19)

將方程式(11-2.7)、(11-2.8)、(11-2.9)及(11-2.10)加以整理，且假設，則可以得到

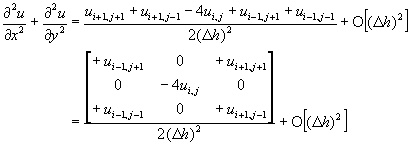    (11-2.20)

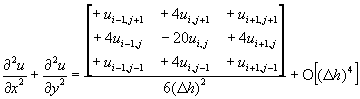                 (11-2.21)

利用這種方法將原來的偏微分方程式改寫成的差分方程式，由於只用到前一時間所得到的資料，因此，稱為顯式差分法(Explicit Form)。顯式差分法在使用上應特別注意穩定性的問題，下一節將以實際範例作說明。

第三節  顯式有限差分近似法之穩定性

        考慮最簡單的拋物線偏微分方程式或暫態熱傳導方程式

                                  (11-3.1)

首先將所考慮的偏微分方程式控制空間轉換成差分格子的形式，如圖11-2所示，其中ui,n表示在時間t = tn時在x = xi位置的函數值。

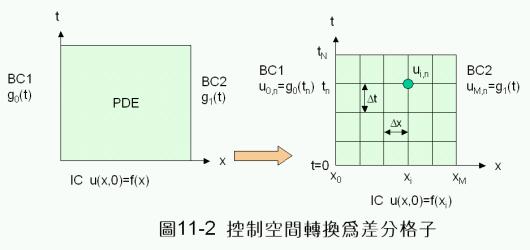
其次，將方程式(11-3.1)改寫成顯式差分方程式，可以得到

                                                           (11-3.2)

定義，則方程式(11-3.2)及對應的邊界條件可以簡化成

                                                     (11-3.3)

          IC.         ui,0=f(xi)

          BC1.        u0,n+1=g0(tn+1)

          BC2.        uM,n+1=g1(tn+1)

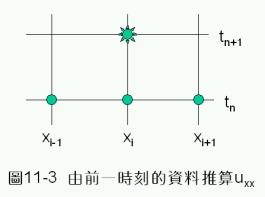
方程式(11-3.3)執行計算時，由前一時刻的三點資料，如圖11-3以圓點表示者，即可以求得下一時刻的函數值，如圖中星狀點所示。但利用程式(11-3.3)執行計算時，所選定的參數會影響計算的準確度及穩定性，應特別注意。

令方程式(11-3.3)的解可以表示為，然後，代回方程式(11-3.3)，可以得到

由於，代入上式中，整理後可以得到

                                                      (11-3.4)

又因為，因此，可以得到的解為

                                                                (11-3.5)

由於在任何及情況下，都必須是有限值。因此，可以得到的解存在且有意義的條件為

                                                                             (11-3.6)

由於最大值為1，最小值為0﹔因此，可以推論滿足上式的條件為。另外，由泰勒級數展開式，可以得到方程式(11-3.3)的差分化誤差為

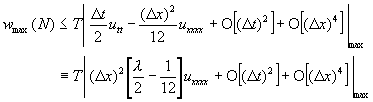
因此，可知當時，差分化誤差為。但當的特定值時，差分化誤差會變成為，積分準確度會更佳。

例11-1  暫態熱傳導

        考慮一無限平板，在時間為零時，其溫度分布為f(x)=0﹔當時間大於零時，平板兩側溫度分別為g0(t)=100及g1(t)=100。此平板之溫度變化可以用以下的拋物線偏微分方程式描述之。

                          

1.      試將此偏微分方程式改寫成差分方程式。

2.      利用Excel撰寫程式，描述積分結果。

 [解]        

1.      所得到的差分方程式為

       

IC.        ui,0=f(xi)=0

BC1.         u0,n+1=g0(tn+1)=100

BC2.         uM,n+1=g1(tn+1)=100

2.      將差分方程式寫成Excel程式，如下圖所示。詳本書所附光碟。

程式編寫方法:

1.      先規劃好dx、dt及l之位置。

2.      於C2位置編寫程式碼﹔C2=I2/F2/F2。

3.      規劃程式所需的表格格式。

4.      於D7位置編寫程式碼﹔D7=$C$2*C6+(1-2*$C$2)*D6+$C$2*E6。

5.      將D7複製到(D7..L26)。

6.      使用時更改I2位置的dt值，程式即自動計算。

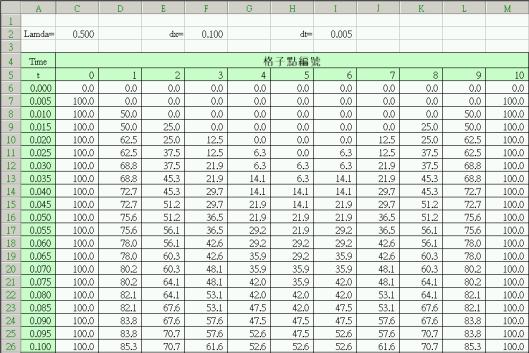
使用這個Excel程式時，應該要特別注意觀察當l值由小變大，對計算結果的影響。此外，也應該要注意當l>2時，會產生何種計算結果。

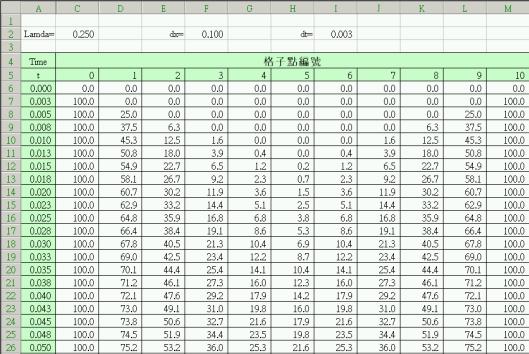
以上計算顯示當時，計算進行基本上都是穩定的。取時，計算結果將呈現震盪情況，如下圖所示。

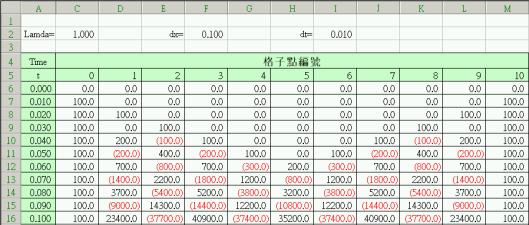
由於平板的溫度一定呈穩定變化，計算產生震盪現象，即證明所選擇參數有誤。當所選擇的積分步伐使得l>2時，會產生震盪現象的原因，是由於建立差分方程式時，所引進的誤差所致。由於，因此，可以推論，在使用差分法求解微分方程式時，並不是一昧將時間及空間分割成越多小段越好，而是應該利用作為決定積分步伐的判斷依據。

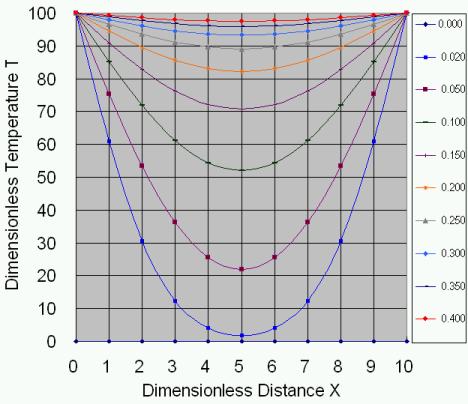
圖11-4  暫態熱傳導的溫度變化

第四節  隱式有限差分近似法

上二節中所介紹的顯式有限差分法，由於使用前一時刻的函數值來計算微分值，並作為此刻的推估值，必然會產生微量誤差，當計算重複執行而未加以修正，則所產生的誤差將會逐漸累增，因此，必須考慮計算的穩定性問題。若將方程式(11-3.2)的差分表示式，更改成使用所考慮時刻的資料計算當時的微分值，如圖11-5所示﹔則得到

                                                   (11-4.1)

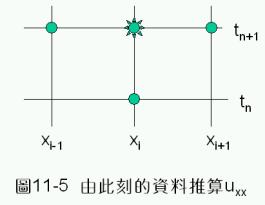
定義，則上一方程式及對應的邊界條件可以簡化成

                                              (11-4.2)

IC.        ui,0=f(xi)

BC1.         u0,n+1=g0(tn+1)

BC2.         uM,n+1=g1(tn+1)

在時間t=tn時，將邊界條件代入，可以將方程式(11-4.2)寫成以下的三對角線方程式

   

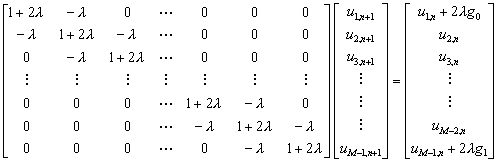
                                                                                                                       (11-4.3)

這種三對角線矩陣方程式，可以利用本書第四章所介紹的上下分解方法求解。這種方法具有絕對穩定性，且其計算過程不會因為選擇的值而造成震盪現象。

科瑞克-尼可森隱式差分法(Crank-Nicolson Method)

以上所介紹的方法中，顯式差分法是將uxx利用前一時刻所得到的資料作差分法表示﹔隱式差分法是將uxx利用同一時刻所得到或所要求解的資料作差分法表示。由於時間方向的差分，基本上應該代表在二時刻間某一時間點的平均微分值，因此，不論顯式積分法或隱式積分法都有過與不及的缺憾。科瑞克-尼可森隱式差分法則是將uxx利用前述二種差分法的某一種平均值來表示。如圖11-6。

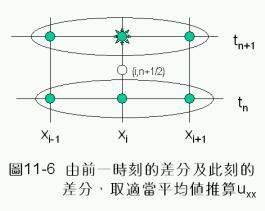
考慮如方程式(11-3.1)所表示之拋物線偏微分方程式

採用以上所說明的邏輯，並利用以下的差分表示方法﹔

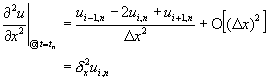
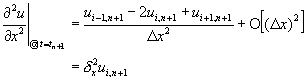
若將uxx利用前後二時間點的兩種差分法，取某一平均值表示。則可以將uxx寫成

                                                           (11-4.4)

代回微分方程式(11-3.1)，可以將微分方程式改寫成以下絕對穩定的差分方程式

                 (11-4.5)

其中。應注意當時即為顯式差分法﹔當時稱為科瑞克-尼可森隱式差分法一般表示式。

方程式(11-4.5)經整理以後，可以得到

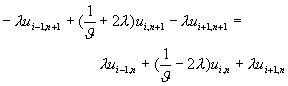                                      (11-4.6)

方程式(11-4.6)中，當時，即稱為科瑞克-尼可森隱式差分法。此時，方程式(11-4.6)可以進一步簡化及整理成

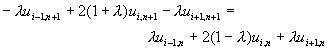                            (11-4.7)

在時間t = tn時，將邊界條件代入，修正第一個及最後一個方程式，即可以將方程式(11-4.6)寫成以下的三對角線方程式

                                                                            (11-4.8)

其中

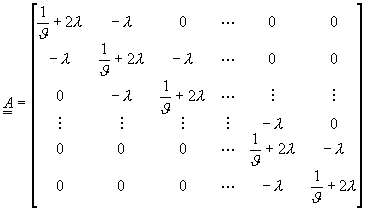
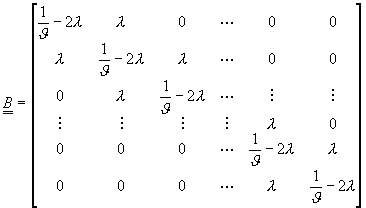
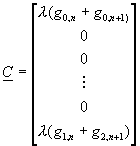
這種三對角線矩陣方程式，可以利用本書第四章所介紹的上下分解方法求解。這種差分方法因為具有絕對穩定性，其計算過程不會因為選擇的值而造成震盪現象。

佛希施及瓦梭(Forsythe & Wasow)證明當時，差分化捨去誤差為。當且時，差分化捨去誤差得到最小值，為。佛希施及瓦梭所提供的參數值，理論上雖然可以提供較高計算準確度，但其缺點是積分位置並不一定在所想要列表的位置，通常需再作內差處理，以便輸出計算結果。所以一般較少被使用。

第五節  絕對穩定的顯式有限差分程序

隱式差分法具有絕對穩定性，但卻需要較複雜的計算。第二節所介紹的單一步驟顯式差分法計算簡單，但卻有l<1/2穩定性限制的考量。

除了第二節所介紹的顯式差分法以外，以下介紹幾種沒有這種穩定性限制的顯式差分法。

督福特-法蘭克法

督福特-法蘭克法(Dufort-Frankel Method)利用三個積分步驟的資料建構差分方程式，如圖11-7所示，其差分表示式為

                                           (11-5.1)

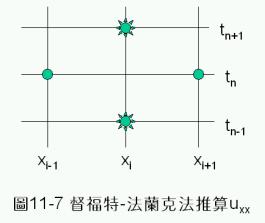
這種方法其實就是將時間差分及空間差分都利用前一步驟的時間點建立。其中空間差分是利用t=tn所得到的資料建立﹔時間差分則利用t=tn-1及t=tn+1的資料建立在t=tn時的微分平均值。利用這種方法由於需使用前二時間點上的資料，在編寫程式時，第一步驟可以先利用顯式差分法計算t=t1的值﹔然後，由t=t2開始，即利用督福特-法蘭克法的差分方程式(11-5.1)作計算。

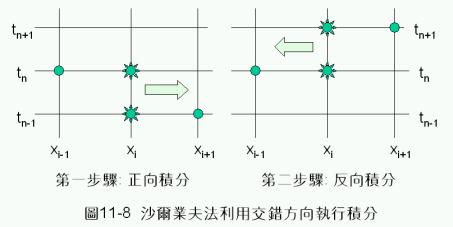
沙爾業夫法

督福特-法蘭克法雖然使用前二時間點的資料，建構差分方程式，已經明顯改善顯式差分法的缺點。但這種方法並未善用全部已經更新的資料。

沙爾業夫法(Saul’yev Method)就是進一步改善督福特-法蘭克法的策略，將已經獲得的資料妥善利用。其做法基本上是利用交錯方向執行積分，如圖11-8所示，積分時第一步驟由x=0開始，採用x正方向積分﹔第二步驟由x的最大值開始，採用x反向積分。執行積分時，以成對方式進行，一次正向積分，一次反向積分。其差分表示式為

                                              (11-5.2)

                                     (11-5.3)

拉金法

拉金法(Larkin Method)與沙爾業夫法相似，利用交錯方向執行積分，如圖11-9所示，積分時由x=0開始，採用x正方向積分一次﹔在同一時間點，再由x的最大值開始，採用x反向再積分一次。然後，取其平均值作為函數近似值。其差分表示式為

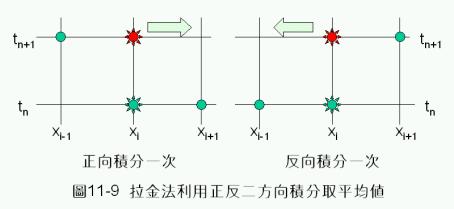
                                           (11-5.4)

                                              (11-5.5)

                                                                       (11-5.6)

第六節  二維及三維偏微分方程式

二維拋物線偏微分方程式

考慮二維拋物線偏微分方程式的典型實例—二維熱傳導問題

                                                                                     (11-6.1)

仿照前面各節的說明，可以將方程式(11-6.1)改寫成差分方程式。

顯式差分法

方程式(11-6.1)改寫成顯式差分方程式時，只要將t方向往前邁進一步，x及y方向的導函數則利用已有資料計算之。

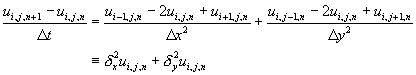        (11-6.2)

使用顯式差分法，由於計算簡單，此處不再詳加說明其計算方法。但應注意，使用顯式差分法時，要注意其穩定條件為

                                                                      (11-6.3)

隱式差分法

方程式(11-6.1)改寫成隱式差分方程式時， x及y方向的導函數要利用tn+1的資料計算之。

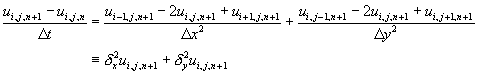 (11-6.4)

為了簡化分析起見，若假設且﹔則方程式(11-6.4)可以整理成為

      (11-6.5)

所得到的差分方程式每一方程式有五項未知數，無法利用三對角線方程式的解法求解，但可以利用本書第四章所介紹的高斯消去法或高斯-賽德迭代法求解。一般而言，利用高斯消去法由於會使計算誤差累加，重複計算將使誤差逐漸增大﹔當我們將及取較小的值，希望得到較高計算準確度時，卻要面對解方程式的計算誤差累增的困擾。但若利用高斯-賽德迭代法計算，由於誤差不會累加，通常能得到較滿意的結果。這種方法為絕對穩定的方法，但計算較麻煩，是其主要缺點。

道格拉斯隱式交替差分法

方程式(11-6.1)改寫成隱式差分方程式時，如上一小節所討論，由於所得到的差分方程式必須利用完整的矩陣方程式求解，而無法使用效率較好的三對角線矩陣解法。為了改善這種缺點，道格拉斯(Douglas)乃提出隱式交替差分法，引進一個在t = tn+1/2時的中間步驟變數v。首先在t = tn+1/2時，計算 x方向的差分，y方向的導函數則利用t = tn時的資料計算之。其次，再在t = tn+1時計算 y方向的差分，x方向的導函數則利用前一中間步驟t = tn+1/2的資料計算之。

道格拉斯隱式交替差分法寫成差分方程式如下:

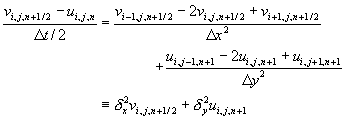                               (11-6.6)

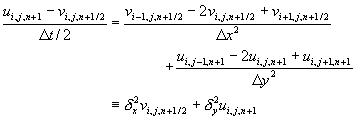                     (11-6.7)

整理成三對角線差分方程式形式，得到

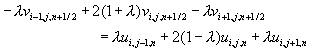                                (11-6.8)

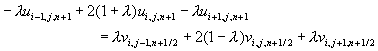               (11-6.9)

計算時，首先利用方程式(11-6.8)計算在t = tn+1/2時的中間步驟變數v。然後，利用方程式(11-6.9) 計算下一時刻 (亦即在t = tn+1時) 的結果u。計算方程式(11-6.8)及方程式(11-6.9)時，都可以利用本書第四章所介紹的三對角線方程式解法求解。與隱式差分法比較，這種方法效率高且處理容易。

三維拋物線偏微分方程式

其次，考慮三維拋物線偏微分方程式的典型實例—三維熱傳導問題

                                                                    (11-6.10)

仿照前面各節的說明，可以將方程式(11-6.10)改寫成差分方程式。

科瑞克-尼可森隱式差分法(Modified Crank-Nicolson Method)

首先，對x方向作科瑞克-尼可森隱式差分法處理，計算求出中間結果v:

        (11-6.11)

其次，再對y方向作科瑞克-尼可森隱式差分法處理，計算求出中間結果p:

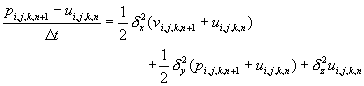              (11-6.12)

最後，再對z方向作科瑞克-尼可森隱式差分法處理，計算求出結果un+1:

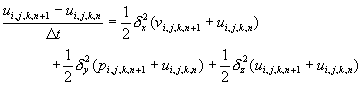               (11-6.13)

這些差分方程式都可以利用三對角線方程式的解法求解。

布萊恩隱式差分法(Brain Method)

首先，在t = tn+1/2時，先對x方向作隱式差分法處理，計算求出中間結果v:

             (11-6.14)

其次，再在t = tn+1/2時，對y方向作隱式差分法處理，計算求出中間結果p:

        (11-6.15)

最後，再對z方向作隱式差分法處理，計算求出結果un+1:

 (11-6.16)

這些差分方程式也都可以利用三對角線方程式的解法求解。

同時含有一次微分及二次微分的偏微分方程式

在圓柱座標及球形座標中，一次微分及二次微分常常同時存在。其處理方式，可以仿照以下的實例處理。

                                  (11-6.17)

第七節  邊界條件與差分方程式

考慮拋物線偏微分方程式，可能的邊界條件可區分為以下三大類。

第一類邊界條件:   應變數u在邊界上為定值。例如，在物體表面溫度等於100℃，或在流體表面濃度等於C0。其一般表示式為u = g。

第二類邊界條件: 應變數u在邊界上的導函數為定值，其中un表示垂直邊界方向的導函數，us表示切線方向的導函數。例如，在傳熱面上有一定的熱通量將熱量傳遞給傳熱面﹔或管壁作斷熱或絕熱處理，使其熱通量為零。其一般表示式為

第三類邊界條件: 應變數u在邊界上的導函數為定值，其中un表示垂直邊界方向的導函數，us表示切線方向的導函數。例如，在流體介面的質傳滲透率等於表面對流所帶走的量﹔或傳熱面的熱傳導通量等於對流熱傳所帶走的熱量。其一般表示式為

考慮二維拋物線偏微分方程式，若使用差分法解偏微分方程式時，邊界條件為第一類邊界條件，直接可以宣告函數值，是最簡單的情況。若邊界條件是第二類或第三類邊界條件時，由於邊界條件含有導函數，必須作適當處理。假設偏微分方程式的邊界條件為

         , 在x=0處                                                             (11-7.1)

針對鄰近於邊界的點u1,j，可以利用泰勒級數展開，得到

                                   (11-7.2)

                                   (11-7.3)

由方程式(11-7.2)可以得到uxx的表示式為

                                               (11-7.4)

又將方程式(11-7.2)及方程式(11-7.3)相加及相減，分別可以得到uxx及ux的表示式為

                                           (11-7.5)

                                                            (11-7.6)

由於邊界條件為，利用方程式(11-7.6)寫成差分式，可以得到

                                                                   (11-7.7)

或整理得到

                                                               (11-7.8)

將方程式(11-7.8)代入方程式(11-7.5)中，將u2,j消去，可以得到uxx的表示式為

                                             (11-7.9)

因此，二維拋物線偏微分方程式改寫成差分方程式時，在邊界上的條件可以寫成

    

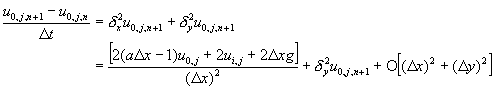
                                                                                                                   (11-7.10)

非規則邊界的處理

        以上所介紹的邊界條件處理原則，基本上都是考慮邊界正好落在格子點上的情況。但如遇到邊界並非正好在格子點上，或邊界呈非規則形狀時，如圖11-12，可以針對鄰近格子點作泰勒級數展開，加以處理。

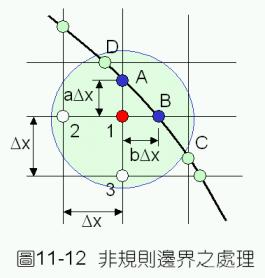
以圖11-12為例，最接近點1的邊界位置為A及B，鄰近的格子點為2及3。分別作泰勒級數展開，可以得到

                                          (11-7.11)

                                          (11-7.12)

                                              (11-7.13)

                                              (11-7.14)

將方程式(11-7.11)及方程式(11-7.12)相加，再加上方程式(11-7.13)乘以a及方程式(11-7.14)乘以b，可以得到在編號1的點上之二階導函數為

                                                                                                           (11-7.15)

第八節  特徵值問題

偏微分方程式常利用分離變數法(Separation of Variables)來求解，是工程應用上最常使用方法之一。利用分離變數法解偏微分方程式時，會將原為分方程式解離成二組或更多組含有任意參數l的常微分方程式。再利用邊界條件決定這些未定參數l，以建立有意義的解答。

史特姆-陸亦威爾(Sturm-Liouville)方程式即是利用分離變數法所得到常見的常微分方程式，其一般表示式為

                                   (11-8.1)

                      

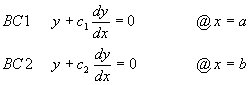
其中函數p(x)、q(x)及r(x)為已知的函數，且在所考慮的區間(a,b)間為連續函數，且r(x) > 0。此方程式只有在特定的l值才有解﹔此特定l值即稱為方程式的特徵值﹔對應的解答稱為特徵函數。

為了簡化說明起見，首先假設p(x)=0，且c1 = c2 =0，a = 0，b = 1。則簡化後的方程式變成

                                    (11-8.2)

                       

利用有限差分法解方程式(11-8.2)時，首先將x區間分割成n個小區間，並令以下變數

xk = h k，      h=1/(n+1)

y(xk)=uk，     u0 = un+1= 0

然後將方程式(11-8.2)改寫成差分方程式

                                                        (11-8.3)

或寫成矩陣形式為

                                                                                         (11-8.4)

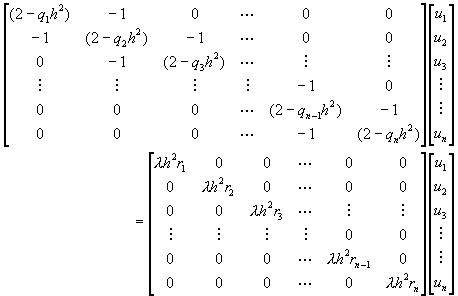     (11-8.5)

令，且，則可將方程式(11-8.4)所表示的矩陣方程式，改寫成

                                                                                                (11-8.6)

由本書第四章的說明可知，方程式(11-8.6)的解答為矩陣A的代數特徵值問題，其數值解法詳見本書第四章。方程式(11-8.6)總共可以得到N個不同的特徵值。利用這些特徵值，可以讓均勻微分方程式建立N個獨立的解。其實際應用，以下例加以說明之。

第九節  配重殘值法

考慮設計問題-XI的流體薄膜吸附問題。此問題之數學模式為

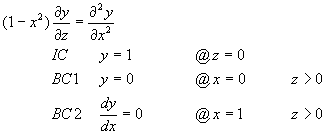                            (11-9.1)

仿照第十章常微分方程式所介紹的配重殘值法(Method of Weighted Residuals, MWR)，令此偏微分方程式的N階近似解為一多項式基礎函數的配重和。由於基礎函數ui(x)必須滿足偏微分方程式的均勻邊界條件(即常數項為零的邊界條件)，由於在本例子中

y(0)=0     y’(1)=0                                                                               (11-9.2)

因此，可以將多項式基礎函數寫成

                                                                             (11-9.3)

                                                       (11-9.4)

其中u0(x，z)為滿足邊界條件及偏微分方程式的函數，基礎函數ui(x)只為x的函數，係數ai(z)為z的函數。將此基礎函數代入偏微分方程式(11-9.1)中，利用配重殘值法求解ai(z)。

如第十章所述，配重殘值法的基本觀念，是利用一組多項式表示近似於問題的正確解，將正確解與近似解的誤差殘值，乘以適當的配重函數後，使其總和或積分值最小化，以達到最接近正確解的目標。微分方程式(11-9.1)的殘值為

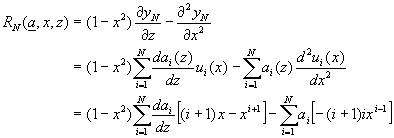             (11-9.5)

葛勒金法(Galerkin’s Method)

葛勒金法的配重函數為，亦即，RN與ui正交﹔

                                       (11-9.6)

將方程式(11-9.5)代入方程式(11-9.6)中，經整理後可以得到矩陣方程式

                                                                                          (11-9.7)

                               (11-9.8)

                                               (11-9.9)

未定係數陣列a可以由方程式(11-9.7)求得。首先將方程式(11-9.7)改寫成方程式(8-9.8)的形式

                                                                                  (11-9.10)

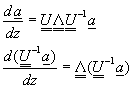                                                                       (11-9.11)

仿方程式(8-9.8)的處理方式，解方程式(11-9.11)，可以得到

                                                                         (11-9.12)

計算策略

利用葛勒金法及特徵矩陣求解微分方程式的方法，可以整理如下:

1.      先將所要求解的問題，表示成方程式(11-9.4)的標準形式。

2.      代回微分方程式中，建立殘值RN的表示式，如方程式(11-9.5)。

3.      由起始條件求出a0=a (z=0)，使用葛勒金法

         (11-9.13)

其中u0(x,0)=1，代入上式，並利用Cji之定義方程式(11-9.8)，可將上式改寫成

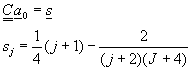                                                             (11-9.14)

4.      依方程式(11-9.7)的定義，建立矩陣A。

5.      求解矩陣A的特徵值，並建立其特徵矩陣U。

6.      利用方程式(11-9.12)，計算a。

a.                                        首先將與a0乘積放置在陣列w1中﹔

b.                                        再將w1的第i個元素除以特徵值li，放置在陣列w2中﹔

c.                                        然後，計算。

7.      利用方程式(11-9.4)計算y。

正交配置法(Orthogonal Collocation Method)

利用正交配置法解偏微分方程式(11-9.1)時，第N個基礎函數可以利用配置點xi上的函數值y(xi,z)及邊界條件y(0,z)=y0=0及y(1,z)=yN+1來表示。起始條件y(xi,0)可以直接寫成配置點上的起始條件﹔

y(xi,0)=1          i=1,2,….,N     

或

                                                                                     (11-9.15)

由於使用正交配置法時，近似函數在配置點上的殘值均為零。利用第十章所介紹的微分操作矩陣，可以將偏微分方程式改寫成

                                                                      (11-9.16)

其中Bji為二次導函數操作矩陣，詳第十章說明。

邊界條件可以寫成

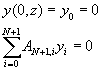                                                                                (11-9.17)

將方程式(11-9.17)的邊界條件，仿第十章說明，代入方程式(11-9.16)中，經整理後得到

                                                                                          (11-9.18)

或

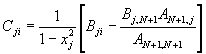
方程式(11-9.18)的解為

                                                                        (11-9.19)

計算策略

利用正交配置法及特徵矩陣求解微分方程式的方法，可以整理如下:

1.      先將所要求解的問題，表示成方程式(11-9.4)的標準形式。

2.      代回微分方程式中，建立殘值RN的表示式，如方程式(11-9.5)。

3.      由起始條件仿方程式(11-9.15)，建立y0。

4.      利用正交配置法建立微分操作矩陣A及B。

5.      依方程式(11-9.18)的定義，建立矩陣C。

6.      求解矩陣C的特徵值，並建立其特徵矩陣U。

7.      利用方程式(11-9.19)，計算y。

a. 首先將與y0乘積放置在陣列w1中﹔

b. 再將w1的第i個元素除以特徵值li，放置在陣列w2中﹔

c. 然後，計算。

參考文獻

1.       Ames, W. F., “Numerical Methods for Partial Differential Equations”, 2nd Ed., Academic Press, New York, (1977).

2.       Bird, R. B., W. E. Stewart, and E. N. Lightfoot, “Transport Phenomena”, Wiley, (1960)

3.       Brian, P. L. T., “A Finite-Difference Method of Higher Order Accuracy for the Solution of Three-Dimensional Transient Heat Conduction Problems”, AIChE J., Vol. 7, pp.367-370, (1961).

4.       Carnahan, B., H. A. Luther, and J. O. Wilkes, “Applied Numerical Methods”, John Wiley, New York, (1998).

5.       Crank, J., “The Mathematics of Diffusion”, Clarendon Press, (1957).

6.       Crank, J., and P. Nicolson, “A Practical Method for Numerical Evaluation of Solution of Partial Differential Equations of the Heat Conduction Type”, Proc. Camb. Phil. Soc., Vol. 43, pp.50-67, (1947).

7.       Douglas, J., “Alternating Direction Method for Three Space Variables”, Numerische Mathematik, Vol. 4, pp. 41-63, (1962).

8.       Dufort, E. C., and S. P. Frankel, “Stability Conditions in the Numerical Treatment of Parabolic Differential Equations”, Math. Tables Aids Comput., Vol.7, pp. 135-152 (1953).

9.       Finlayson, B. A., “The Method of Weighted Residuals and Variational Principles”, Academic Press, (1972).

10.    Saul’yev, V. K., “Integration of Equations of Parabolic Type by the Method of Nets”, Macmillan, New York, (1964).

11.    Larkin, B. K., “Some Stable Explicit Difference Approximations to the Differential Equations”, Math. Of Comp., Vol. 18, pp. 196-202, (1964).

12.    Villadsen, J., and M. L. Michelson,”Solution of Differential Equation Models by Polynomial Approximation”, Prentice Hall, (1978).

 

回首頁     回第三部

CHEER  Copyright 2001 by Dr. Ron Hsin Chang