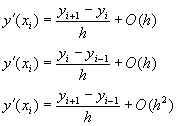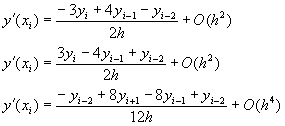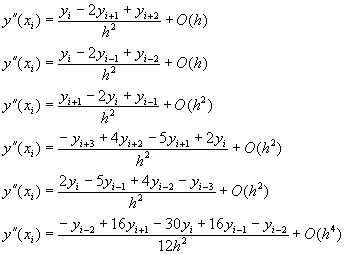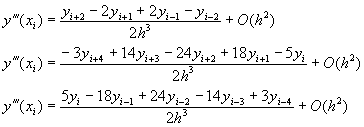回首頁     回第三部     下一章

第九章　常微分方程式—邊界值問題

常微分方程式一邊界條件的定義位置分類，可分成初值問題(I.V.P)及邊界值問題(B.V.P)，其中初值問題的數值解法我們已在第八章中詳加討論。本章中，我們將討論幾種解邊界值常微分方程式的解法。

邊界值常微分方程式的解法基本上可分成三大類：

(1) 初值法：包括投射法(Shooting)及加成法(Superposition)

(2) 有限差分法(Finite difference method)

(3) 配重殘值法(Method of Weighted Residuals)

所謂初值法基本上是將邊界值常微分方程式問題視為一組聯立的初值常微分方程式問題，再利用迭代法求解。初值法可大致分成投射法、多重投射法及加成法三類，以下只對投射法作討論。加成法及多重投射法雖常見於商業化程式，但由於涉及較多數學處理，故此處不加以討論，有興趣讀者請參閱[5，6]。在第六章中，我們曾討論過利用差分表示導函數，若進一步將微分方程式中的導函數用差分表示，建立一組差分方程式，即稱為有限差分法。配重殘值法基本想法是利用一組近似函數加上配重函數(請回顧第六章所提高斯積分法)來表示微分方程式的近似解，使得函數積分殘值達到最小化，即為最佳近似解。我們將在本章中討論初值法及有限差分法，配重殘值法則單獨於第十章中詳加討論。

第一節  投射法—線性問題

投射法(Shooting Method)屬於常微分方程式解法中的初值法的一種。首先考慮線性二次常微分方程式

                                          (9-1.1)

        BC1         x＝a時，

        BC2         x＝b時，

其中k1，k2，h1，h2，a及b均為常數，且

                                                                 (9-1.2)

由於線性常微分方程式具有加成性，首先將函數y(x)寫成y1及y2兩部分的加成:

y(x) = y(x,s) = y1(x) + sy2(x)                                                                (9-1.3)

其中s為任一常數，y1(x)及y2(x)分別為下列初值常微分方程式的解:

                                           (9-1.4)

        IC1          x＝a時，

        IC2          x＝a時，

                                                (9-1.5)

        IC3          x＝a時，

        IC4          x＝a時，

其中C1及C2均為常數。由於y＝y1＋sy2，因此，根據原微分方程式的第一個邊界條件，得到

或

C1 h1－C2 k1＝1                                                                                      (9-1.6)

而由原方程式的第二個邊界條件，則可以得到

解上式，得到s的表示式為

                                                                   (9-1.7)

因此，解線性邊界值常微分方程式的執行策略可歸納如下：

1.   將原邊界值BVP常微分方程式(9-1.1)轉換成初值IVP常微分方程式(9-1.4)及(9-1.5)。

2.   令C1為一任意值 [或根據方程式(9-1.6)作適當猜測]。

3.   利用方程式(9-1.6)求出C2。

4.   將IVP常微分方程式(9-1.4)積分，求得y1(b)及y1’(b)。

5.   將IVP常微分方程式(9-1.5)積分，求得y2(b)及y2’(b)。

6.   利用方程式(9-1.7)求得s。

7.   利用方程式(9-1.3)建立y與x之關係。

第二節  投射法—非線性問題

考慮二次非線性常微分方程式及其邊界條件為

y”＝f(x，y，y’)， a＜x＜b                                                                        (9-2.1)

        BC1  x＝a，  -k1y’＋h1y＝α

        BC2  x＝b，  k2y’＋h2y＝β

其中k1，k2，h1，h2，α及β均為常數，且

k1h1≧0﹔｜k1｜＋｜h1｜≠0

k2h2≧0﹔｜k2｜＋｜h2｜≠0

h1＋h2＞0

相對應的初值問題為

u” = f(x，u，u’)﹔a＜x＜b                                                                 (9-2.2)

                IC1          x＝a時， u(a)＝αC1＋sk1

                IC2          x＝a時， u’(a)＝αC2＋sh1

其中IC1及IC2設為u(a)＝αC1＋sk1及u’(a)＝αC2＋sh1，目的是讓第二項sk1及sh1代入BC1後，會相減而消失。同理，αC1及αC2也是要讓二式相加變成α，以簡化後續處理。將上式代回方程式(9-2.1)可以得到

C1h1－C2k1＝1

        將IVP方程式(9-2.2)積分至x＝b時，必須滿足原微分方程式的第二個邊界條件，即殘值R(s)必須為0。

R(s)＝k2u’(b﹔s)＋h2u(b﹔s)－β＝0                                                  (9-2.3)

R(s)為一非線性方程式，可以利用牛頓拉福森法解上式求s，迭代式為

                                                                                  (9-2.4)

由方程式(9-2.3)，得為

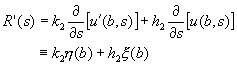                                                   (9-2.5)

其中

                                                                                      (9-2.6)

                                                                                     (9-2.7)

將方程式(9-2.2)改寫成矩陣型式的一次聯立微分方程式，得

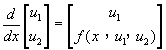                                                                     (9-2.8)

       I.C.          x＝a時，[u1，u2]T＝[αC1＋sk1，αC2＋sh1]T

其中u1＝u(x﹔s)﹔u2＝u’(x﹔s)。將上式對s微分，由於

因此，利用方程式(9-2.6)及方程式(9-2.7)的ξ及η定義，可以得到以下結果

                                                                                                  (9-2.9)

                                      (9-2.10)

或寫成矩陣型式

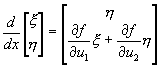                                                                      (9-2.11)

                I.C.          x＝a時，[ξ，η]T＝[k1，h1]T

將上式積分，即可求得ξ(b)及η(b)，代回方程式(9-2.5)可求得R’(s)。再利用方程式(9-2.4)即可求得新的s值。

        非線性邊界值常微分方程式的投射法執行策略，可歸納如下:

1. 將原BVP常微分方程式(9-2.1)轉換成IVP方程式(9-2.8)。

2. 任意猜測一個C1值。

3. 利用C1 h1－C2 k1＝1求出C2。

4. 任意假設一個s0值。

5. 將IVP常微分方程式(9-2.8)及(9-2.11)積分至x＝b。

6. 利用方程式(9-2.3)及(9-2.5)分別求R(s)及R’(s)。

7. 利用方程式(9-2.4)求sk+1。

8. 重複步驟5～7，直到s收斂為止。

第三節  有限差分法

我們在第六章中曾討論了利用有限差分法求導函數近似值的作法。如果我們將微分方程式中的導函數利用這種表示方法來取代，則可將微分方程式轉換成差分方程式，所得的解可作為原微分方程式的近似解﹔這種方法就稱為有限差分法(Finite Difference Method)。

有限差分法與投射法各有長處，優劣甚難論斷，但一般認為差分法有時略較投射法易於使用。

有限差分法基本上是將BVP微分方程式改寫成差分方程式，將微分方程式的求解變成較簡單的聯立代數方程式，例如，考慮BVP微分方程式

                                                 (9-3.1)

        BC1         x＝a﹔    y＝A

        BC2         x＝b﹔    y＝B

首先將[a，b]區間分割成n等份，使

，        i＝1，2，……，n                                                 (9-3.2)

其中x0＝a，xn＝b，且

                                                                                               (9-3.3)

xi稱為節點(node)，表示要求解yi的位置﹔h稱為積分間距(step size)。

函數y(x)利用泰勒級數展開，得

              (9-3.4)

因此，y(x)的一次導函數可利用一階差分式表示為：

                             (9-3.5)

                                      正向差分

                               (9-3.6)

                                      逆向差分

若將上二式相加，則得y’(x)的二階差分式：

                                       (9-3.7)

        y(x)的二次導函數差分式可由(9-3.4)正負符號兩種表示式相加，可以得到

整理之，得到y”(x)的差分近似表示式為

                                       (9-3.8)

        利用方程式(9-3.7)及(9-3.8)，可將微分方程式(9-3.1)改寫成二階準確度的有限差分近似式

                                        i＝1，2，……，N－1                                          (9-3.9)

其中

                yO＝A，yN＝B

將上式乘以2h2，整理後得

                                    (9-3.10)

其中

               

               

將方程式(9-3.10)改寫成矩陣符號為

                                                                                                  (9-3.11)

其中

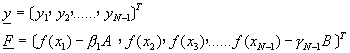
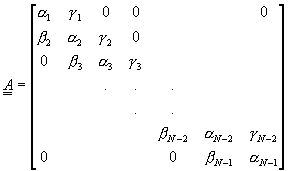
矩陣稱為三對角線矩陣。矩陣方程式的解法可利用本書第四章所介紹的高斯消去法或三對角線矩陣方程式解法求之，即可求得近似解。

[1]

等間距有限差分法一次導函數hy'之表示式

 

編號

乘數

 

不同表示式的係數

 

誤差

101

1

　

-1

1

 

 

 

 

 

　

-1/2

hy"(x)

102

　

-1

1

 

 

 

 

 

　

1/2

103

1/2

　

-3

4

-1

 

 

 

 

　

1/3

h2y'''(x)

104

　

-1

0

1

 

 

 

 

　

-1/6

105

　

1

-4

3

 

 

 

 

　

1/3

106

1/6

　

-11

18

-9

2

 

 

 

　

-1/4

h3yiv(x)

107

　

-2

-3

6

-1

 

 

 

　

1/12

108

　

1

-6

3

2

 

 

 

　

-1/12

109

　

-2

9

-18

11

 

 

 

　

1/4

110

1/12

　

-25

48

-36

16

-3

 

 

　

1/5

h4yv(x)

111

　

-3

-10

18

-6

1

 

 

　

-1/20

112

　

1

-8

0

8

-1

 

 

　

1/30

113

　

-1

6

-18

10

3

 

 

　

-1/20

114

　

3

-16

36

-48

25

 

 

　

1/5

115

1/60

　

-137

300

-300

200

-75

12

 

　

-1/6

h5yvi(x)

116

　

-12

-65

120

-60

20

-3

 

　

1/30

117

　

3

-30

-20

60

-15

2

 

　

-1/60

118

　

-2

15

-60

20

30

-3

 

　

1/60

119

　

3

-20

60

-120

65

12

 

　

-1/30

120

　

-12

75

-200

300

-300

137

 

　

1/6

121

1/60

　

-147

360

-450

400

-225

72

-10

　

1/7

h6yvii(x)

122

　

-10

-77

150

-100

50

-15

2

　

-1/42

123

　

2

-24

-35

80

-30

8

-1

　

1/105

124

　

-1

9

-45

0

45

-9

1

　

-1/140

125

　

1

-8

30

-80

35

24

-2

　

1/105

126

　

-2

15

-50

100

-150

77

10

　

-1/42

127

　

10

-72

225

-400

450

-360

147

　

1/7


陰影部分表示基準點。例如第115號方程式為

[2]

等間距有限差分法一次導函數 h2y" 之表示式

 

編號

乘數

　

不同表示式的係數

　

誤差

201

1

　

1

-2

1

 

 

 

 

　

-

hy"'(x)

202

　

1

-2

1

 

 

 

 

　

-1/12

h2yiv(x)

203

　

1

-2

1

 

 

 

 

　

 

hy"'(x)

204

1/6

　

12

-30

24

-6

 

 

 

　

11/12

h2yiv(x)

205

　

6

-12

6

0

 

 

 

　

-1/12

206

　

0

6

-12

6

 

 

 

　

1/12

207

　

-6

24

-30

12

 

 

 

　

11/12

208

1/24

　

70

-208

228

-112

22

 

 

　

-5/6

h3yv(x)

209

　

22

-40

12

8

-2

 

 

　

1/12

210

　

-2

32

-60

32

-2

 

 

　

1/90

h4yvi(x)

211

　

-2

8

12

-40

22

 

 

　

-1/12

h3yv(x)

212

　

22

-112

228

-208

70

 

 

　

5/6

 

[3]

等間距有限差分法一次導函數 h3y"' 之表示式

 

編號

乘數

　

不同表示式的係數

　

誤差

301

1

　

-1

3

-3

1

 

 

 

　

-2/3

hyiv(x)

302

　

-1

3

-3

1

 

 

 

　

-1/2

303

　

-1

3

-3

1

 

 

 

　

1/2

304

　

-1

3

-3

1

 

 

 

　

3/2

305

1/2

　

-5

18

-24

14

-3

 

 

　

7/4

h2yv(x)

306

　

-3

10

-12

6

-1

 

 

　

1/4

307

　

-1

2

0

-2

1

 

 

　

-1/4

308

　

1

-6

12

-10

3

 

 

　

1/4

309

　

3

-14

24

-18

5

 

 

　

7/4

 

[4]

等間距有限差分法一次導函數 h4yiv 之表示式

 

編號

乘數

　

不同表示式的係數

　

誤差

401

1

　

1

-4

6

-4

1

 

 

　

-2

hyv(x)

402

　

1

-4

6

-4

1

 

 

　

-1

403

　

1

-4

6

-4

1

 

 

　

-1/6

h2yvi(x)

404

　

1

-4

6

-4

1

 

 

　

1

hyv(x)

405

　

1

-4

6

-4

1

 

 

　

2

 

以上各表所列資料是利用有限差分法解常微分方程式時常見的差分近似式歸納表，列出所有表示式的目的，是讓使用者建立邊界條件表示式時，易於使用。其中最常被使用的表示式，依表中所列，整理如下：

 

 

[A] 一次導函數

 

 

 

[B] 二次導函數

[C] 三次導函數

[D] 四次導函數

第四節  邊界條件與有限差分法

以上介紹了如何將微分方程式利用差分法表示，並且整理出各種差分表示法供參考使用。除了微分方程式的差分化以外，要解微分方程式，還得了解如何將邊界條件改寫成對應的差分表示法。以下以線性二次常微分方程式為例加以說明。

                                                                  (9-4.1)

        BC1       x＝0，   

        BC2        x＝1，   

仿上節說明，可將微分方程式(9-4.1)改寫成差分近似式

 ， i＝1，2，……，N-1                     (9-4.2)

邊界條件則可以有不同的處理方式，以下分別說明之。

[A] 一階近似法　O(h)

邊界條件中的導函數y’(0)及y’(1)分別用一階正向差分及逆向差分表示，

                                                                                       (9-4.3)

                                                                                   (9-4.4)

代回BC1及BC2，經整理後，可分別求得y0及yN為

                                              (9-4.5)

                                    (9-4.6)

將y0及yN代回方程式(9-4.2)，並將(9-4.2)改寫成矩陣型式，得到

                                                                                                 (9-4.7)

其中

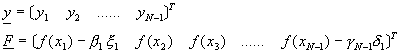
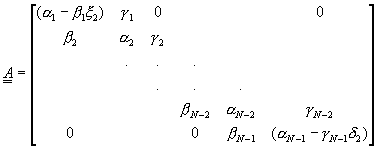
 ， i＝1，2，……，N－1

             

             

               

               

    ，    x0＝0

方程式(9-4.7)基本上與方程式(9-3.11)的形式完全相仿，仍為三對角線矩陣方程式，可以利用相同方法解之。

[B] 二階近似法

邊界條件中的導函數y’(0)及y’(1)，若利用準確度為O(h2)的中央差分式表示，則需分別引入假節點(fictitious nodes) x－1及xN＋1，和對應的函數值y－1及yN＋1：

                                                                                      (9-4.8)

                                                                         (9-4.9)

代回BC1及BC2，分別求解假設的y－1及yN＋1，得到

                                (9-4.10)

                            (9-4.11)

代回方程式(9-4.2)，並令i＝0，1，2，……，N，改寫成矩陣型式後得到

                                                                                                  (9-4.12)

其中

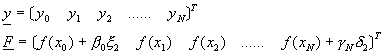
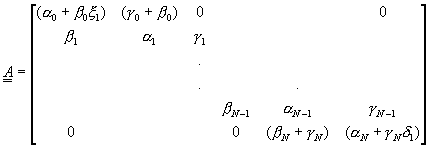
 ，  i＝0，1，2，……，N

              

              

    ，    x0＝0

第五節  非線性常微分方程式

將非線性常微分方程式改寫成差分方程式，所使用的方法，與前面所討論的線性常微分方程式作法完全一樣。但所得到的差分方程式通常為非線性聯立方程式，因此，無法像線性問題般直接用三對角線矩陣方程式求解，而必須利用牛頓迭代法或其他數值方法才能求得近似解。

考慮二次非線性常微分方程式

    ，    a＜x＜b                                          (9-5.1)

        BC1         x＝a，    y＝A

        BC2         x＝b，    y＝B

使用二階差分近似法，則方程式(9-5.1)可以被改寫成以下的差分方程式

                                            (9-5.2)

                i＝1，2，……，N－1

                y0＝A，  yN＝B

若邊界條件為第二類或第三類邊界條件，亦可仿上節方式處理之。方程式(9-5.2)通常為聯立非線性方程式，令

       

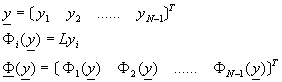
則方程式(9-5.2)可簡寫為

                                                                                                        (9-5.3)

        利用牛頓迭代法解所得到的方程式(9-5.3)，可以得到

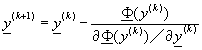                                                                     (9-5.4)

其中亦可利用數值方法求之，也就是利用牛頓割線法解方程式(9-5.3)。此外，亦可利用連續迭代法求。以下以實際例子加以說明。

例9-1             零次恆溫催化反應

以下看似相當容易的常微分方程式，用於描述一球形觸媒粒子內進行零次常溫反應，且主成分趨近於平衡時的濃度分布情況。

                                                               (9-5.5)

        BC1         x＝0                ＝0

        BC2         x＝1                y＝1

試求濃度分布函數y(x)。

[解]　利用二階差分式將原方式改寫成差分方程式，得到

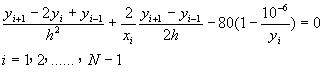                (9-5.6)

邊界條件BC1仿上節處理方式，引入一假節點x－1，則BC1可改寫成差分式。

或。當x＝0時，根據L’Hospital定理，原微分方程式第二項可改寫成

因此，當x＝0時，原微分方程式變成

                                               (9-5.7)

或寫成差分式為

                                          (9-5.8)

由於，代入方程式(9-5.8)，整理之。並將(9-5.8)也改寫成(9-5.3)型式，得到

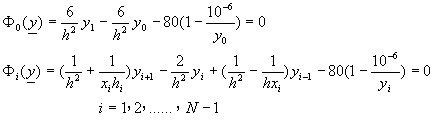
                                                                                            (9-5.9)

以上計有N個聯立方程式，可求解y0，y1，……，yN-1，N個未知數。

參考文獻

1.      Schlichting, H., “Boundary layer theory” , 4th ed., McGraw-Hill, New York, (1960).

2.      Hall, G., and J. M. Watt, “Modern Numerical Methods for Ordinary Differential Equations”, Oxford Univ. Press, Inc., New York, (1976).

3.     Lapidus, L., and J. H. Seinfeld, “Numerical Solution of Ordinary Differential Equations”, Academic Press, New York, (1971).

4.     Caberry, J. J., “Chemical and Catalytic Reaction Engineering”, McGraw-Hill, New York, (1976).

5.      Deuflhard, P., “Recent Advances in Multiple Shooting Techniques” in “Computational Techniques for Ordinary Differential Equations”, Edited by Gladwell, I., and D. K. Sayers, Academic, London, (1980).

6.      Scott, M. R., and H. A. Watts, “Computational Solutions of Linear Two Point Boundary Value Problems via Ortho-normalization”, SIAM K. Numer. Ana., 14, 40 (1977).

7.      Nogotov, E. F., “Applications of Numerical Heat Transfer” Hemisphere, Washington, (1978).

8.      Anderson, D. A., J. C. Tannehill, and R. H. Pletcher, “Computational Fluid Mechanics and Heat Transfer”, McGraw Hill, New York, (1984).

9.      Shoup, T. E., “Applied Numerical Methods for the Microcomputer” Prentice-Hall, London, (1984).

10.    Davis, M. E., “Numerical Methods and Modeling for Chemical Engineers” John Wiley, New York, (1984).

11.    Whitaker, S., “Elementary Heat Transfer Analysis” (1976).

12.   Rohsenow, W. M., and H. Y. Choi, “Heat, Mass, and Momentum Transfer”, Prentice-Hall, Englewood Cliffs, N.J., (1961).

 

回首頁     回第三部     下一章