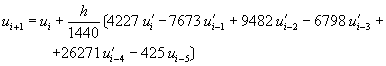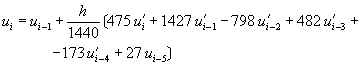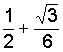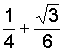回首頁     回第三部     下一章

第八章  常微分方程式—初值問題

工程及科學領域中，許多問題都可以利用微分方程式來描述。微分方程式又可分成偏微分方程式及常微分方程式兩大類。方程式中若只含一個獨立變數的導函數，即稱為常微分方程式﹔否則若含有一個以上獨立變數的導函數，即稱為偏微分方程式。

常微分方程式依其邊界條件分類，又可分成初值問題(IVP, Initial Value Problem)及邊界值問題(BVP, Boundary Value Problem)。例如

IVP：         y(0)＝1，y’(0)＝1                                         (8-0.1)

BVP：        y(0)＝1，y(1)＝2                                           (8-0.2)

其中y’表示(dy／dx)。IVP與BVP的差別在於IVP的邊界條件均定在同一x位置上，但BVP邊界值則定在兩個不同位置上。

        由於描述實際問題所得到的微分方程式，極少能利用解析方法得到理論解，因此，通常需利用數值方法求解。常微分方程式中IVP及BVP的數值解法有相當大的差異，需要完全不同的處理方法，因此，本章首先討論初值問題(IVP)，邊界值問題(BVP)則留待第九章及第十章詳加討論。

        考慮m次常微分方程式

y(m)＝f(x，y，y’，y’’，……，y(m-1))                                                    (8-0.3)

其起始條件為

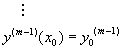
其中f為已知的函數，且y0，y0’，y0’’，……，y0(m-1)均為常數。方程式(8-0.3)通常可改寫成一組一次微分方程式。首先定義一組新的獨立變數y1(x)，y2(x)，……，ym(x)為

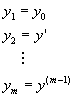                                                                                             (8-0.4)

則方程式(8-0.3)即可被轉換成

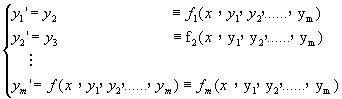                           (8-0.5)

起始條件為

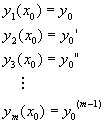
將方程式(8-0.5)寫成向量符號，可以得到

                                                          (8-0.6)

其中

              

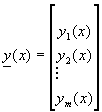
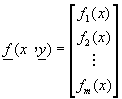
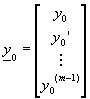
        方程式(8-0.6)可用於表示一個m次常微分方程式，一組次數和為m的聯立微分方程式，或m個一次聯立微分方程式。一般而言，解常微分方程式的方法就是要解方程式(8-0.6)。但為了簡化分析起見，我們首先考慮最簡單的初值問題。

                           (8-0.7)

然後再推展至方程式(8-0.6)的一般情況。

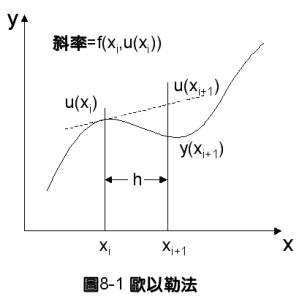
第一節  歐以勒法

歐以勒法(Euler’s Method)是常微分方程式的數值解法中最簡單的一種，效率不高、準確度較差，但卻是說明數值解法運作原理的最佳工具。我們首先考慮方程式(8-0.7)所表示的一次常微分方程式，並將[x0，xN]分割成N個等間距的小區間，使得

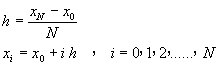                                                          (8-1.1)

h稱為積分間距(step size)。假設y(x)為方程式(8-0.7)的正確解，則利用泰勒定理將y(x)對xi展開，得到

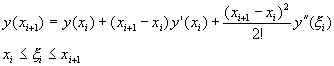                            (8-1.2)

將方程式(8-0.7)代入上式，得到

                                   (8-1.3)

若將上式中h2項截去，即可獲得最簡單的數值方法。令ui＝y(xi)，ui+1＝y(xi+1)，則上式可改寫成

                                    (8-1.4)

此方法即稱為歐以勒法。

        由方程式(8-1.3)可以得知，歐以勒法的截尾誤差為

                                                              (8-1.5)

因此，我們可以預測h值愈小，則計算準確度愈高(在機器準確度以內而言)。但是h值愈小，所需計算時間也愈多。因此，積分間距的適當選擇，在積分方程式的數值解法中，即成為非常重要的步驟。

考慮最簡單的一次常微分方程式

                                                 (8-1.6)

其中λ為一常數。利用歐以勒法，則由方程式(8-1.6)可以得到

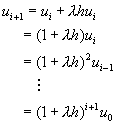                                                                                 (8-1.7)

而方程式(8-1.6)的理論解為

                                                                  (8-1.8)

比較方程式(8-1.7)及(8-1.8)，顯示歐以勒法是以(1+λh)取代exp(λh)。由於任何數字都無法正確地表示成一機器數字，因此，利用u0表示y0亦可能存在捨入誤差，即e0＝(y0－u0)可能不為零。將方程式(8-1.7)中的u0用y0－e0表示，得

                                                                      (8-1.9)

與方程式(8-1.8)比較，得到計算的總誤差為

                                   (8-1.10)

計算的總誤差是由兩部分所組成，前者是由於利用歐以勒法以(1+λh)取代exp(λh)所產生的誤差，後者是由於最初的誤差e0所造成的。很明顯地，如果以上的方程式中｜1＋λh｜＞1，則e0所造成的誤差會快速成長，變成Ei+1的主要部分。因此，要使歐以勒法維持絕對穩定的條件為

－1≦1＋λh≦1或 -2≦λh≦0                                                    (8-1.11)

但此系統要維持不產生震盪的情況，則需0≦1＋λh≦1。否則e0所造成的誤差會成為一正一負的震盪情況。

例8-1             同分異構化反應

Cocks and Egger [1]研究正亞丙基環丙胺(m-propylidenecyclo- propylamine)變成5-乙基-1-梅笠草烯(5-ethyl-1-pyroline)的同分異構化反應，發現此反應為一次反應，其反應速率常數為

       

其中R＝1.9872 cal／g mole。K，T為反應溫度。

        若此一反應在一恆溫管狀反應器中進行，且流動狀況趨近於塞式流動(plug flow)，試計算正亞丙基環丙胺在反應器內的濃度分布。設反應溫度為700。K。反應器滯留時間為200秒及50秒兩種。

[解]

        一次反應的速率表示式為[2]

        －rA＝kCCA

反應器的穩定態質量平衡，可以利用正亞丙基環丙胺在反應器軸向流動的變化量等於反應掉的量表示之，

       

其中nA為反應物的質量流率，與濃度CA及反應溶液的體積流量uT關係為

        nA＝CAuT

定義反應器滯留時間為θ＝VT／uT，VT為反應器總體積，Z為反應器軸向座標，L為反應器總長度，y＝CA／CA0，x＝Z／L，則質量平衡式可改寫成

       

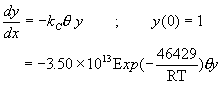
或

利用方程式(8-1.6)的方式表示，λ分別等於－22.365及－5.591。根據定性分析，數值方法穩定條件為－2≦hλ≦0，誤差不會震盪的條件為－1≦hλ≦0。

穩定條件

θ＝200 sec.

θ＝50 sec.

不穩定

h>0.0894

h>0.3577

穩定，但誤差會震盪

0.0447＜h＜0.0894

0.1789＜h＜0.3577

穩定，且誤差不震盪

0＜h＜0.0447

0＜h＜0.1789

由於歐以勒法是所有數值方法中最簡單的一種，因此，本例題的程式設計留供讀者自行完成，並實際驗證上表的結果(參見本章末問題1)。

第二節  阮奇庫塔法

使用最簡單的歐以勒法解微分方程式的時候，計算所使用的方程式(8-1.4)，，所代表的意義是要計算ui+1時，可利用前一點的函數值ui值，加上在前一點處的斜率f(xi,ui)乘上h值來估算。這種方法很明顯的將使積分誤差逐漸累積而蔓延，使得結果的正確性較差，這也是可以預期的。

要改善這種方法，一個基本想法就是在利用前述方法計算ui+1時，在求函數f(xi,ui)的近似值時加以適當修正，考慮在xi至xi＋1中選取幾個特定點，分別計算它的函數值Kj，並加上適當的配重，用以計算及表示f(xi,ui)，這種方法就稱為阮奇庫塔法(Runge-Kutta Method)，其一般表示式可以寫成

                                                                           (8-2.1)

其中為配重因子，n代表所選取xi至xi＋1中的點數，Kj為xi至xi＋1中的某一點的函數f值。Kj可以表示成

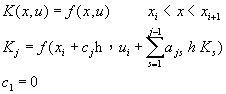                                                      (8-2.2)

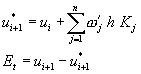
為了便於表達起見，阮奇庫塔法的係數可以用下列的方塊表示法表示：

當m=1時，，且K1 = f(xi,ui)，方程式(8-2.1)可以被簡化成ui+1=ui + hf(xi,ui)，即為上一節所討論的歐以勒法。因此，歐以勒法也可以稱為最低階的阮奇庫塔法。利用方塊表示法表示，即成為

歐以勒法

0

0

 

1

阮奇庫塔法具有以下三點特色：

(1)    阮奇庫塔法為單間距積分法：要求得um+1，我們只需前一點的資料(xm，um)即可。

(2)    使用阮奇庫塔法求解常微分方程式，不需計算f(x，y)的導函數，只需使用f(x，y)函數值即可進行積分運算。

(3)    p階的阮奇庫塔法與泰勒級數比較，至hp均相同﹔但p值隨不同方法而異。

[A]  二階阮奇庫塔法

較高階的阮奇庫塔法方程式中，參數、cj及ajs基本上是利用泰勒級數展開與方程式(8-2.1)比較來求得。例如，當m = 2時，首先將原微分方程式dy/dx=f(x,y)的正確解利用泰勒級數展開，得到

                      (8-2.3)

由於f為x及y的函數，而y又為x的函數，因此，可以再將f’(xi,y(xi))改寫成

                               (8-2.4)

其中下註標i表示第i個點，fx表示f對x的導函數，fy表示f對y的導函數。將方程式(8-2.4)代入方程式(8-2.3)中，並將h3項截掉，得到

                                                               (8-2.5)

在以上各方程式中，y代表正確解，而u則代表數值方法的近似解。

其次，再將xi至xi＋1中的某一點的函數值Kj對xi位置作泰勒級數展開。由於K為x及u的函數，因此，作泰勒級數展開時可以得到

K(x,u)      = f(x,u)            xi<x<xi+1

                = f(xi,ui) + (x-xi) fx(xi,ui) + (u-ui) fy(xi,ui)                              (8-2.6)

由方程式(8-2.2)Kj的定義及方程式(8-2.6)，可以將Kj寫成

K1 = f(xi,ui)                                                                                           (8-2.7)

K2 = f(xi + c2 h , ui + a21 h K1)

       = f(xi + c2 h , ui + a21 h f)

       = fi + h(c2 fx + a21 fy f)i                                                                    (8-2.8)

方程式(8-2.8)中，K2由第二行改寫成第三行時，是利用對xi位置作泰勒級數展開。將以上二方程式代回方程式(8-2.1)，整理後可以得到

                           (8-2.9)

上式與ui+1的泰勒級數展開式(8-2.5)比較，得到以下聯立方程式：

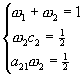                                                                                      (8-2.10)

由於二階阮奇庫塔法總共有四個待定係數w1，w2，c2及a21，但只有上列三個方程式，自由度為1。因此，仍留有一個可自由設定的參數。就m＝2而言，常見的參數設定值如下：

c2

w1

w2

a21

0

1

1

1

亦即二階阮奇庫塔法可以寫成以下兩種型式：

        c2＝；中點法或稱為修正歐以勒法(Modified Euler Method)

                                                        (8-2.11)

或用方塊法表示為

修正歐以勒法

0

0

 

1/2

1/2

 

 

0

1

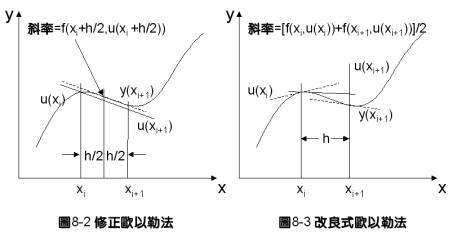
c1＝1；端點平均值法或稱為改良式歐以勒法(Improved Euler Method)

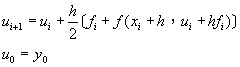                                               (8-2.12)

或用方塊法表示為

改良式歐以勒法

0

0

 

1

1

 

 

1/2

1/2

注意原微分方程式為dy／dx＝f(x，y)，因此，f所代表的物理意義是在(x，y)點處的曲線斜率。故方程式(8-2.11)代表利用[xi，xi+1]的中點斜率進行計算，而方程式(8-2.12)則是利用xi及xi+1兩端點位置的斜率平均值進行計算。

方程式(8-2.12)通常也被稱為預測修正法(Predictor-Corrector Method)，並可以改寫成以下的型式：

預測式：

修正式：                                          (8-2.13)

阮奇庫塔法基本上是一種演導方法，仿以上的做法，可以推出各種不同的阮奇庫塔法。較高階的阮奇庫塔法由於計算費時，除了特殊需要，通常較少被使用。目前最常被使用的阮奇庫塔法有：

(1) 三階庫塔法(3rd Order Kutta Method)

(2) 四階阮奇庫塔法(4th  Order Runge-Kutta Method)，

(3) 阮奇庫塔基爾法(Runge-Kutta-Gill Method)，及

(4) 阮奇庫塔摩森法(Runge- Kutta- Merson Method)。

[B] 三階庫塔法(3rd Order Kutta Method)

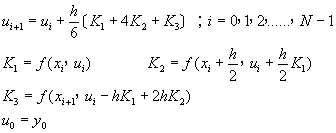                       (8-2.14)

或用方塊法表示為

三階庫塔法

0

0

 

 

1/2

1/2

 

 

1

-1

 

 

 

1/6

2/3

1/6

[C] 四階阮奇庫塔法(4th Order Runge-Kutta Method)

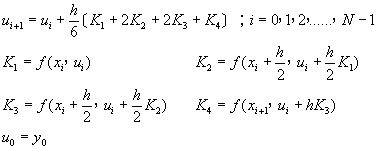            (8-2.15)

或用方塊法表示為

四階阮奇庫塔法

0

0

 

 

 

1/2

1/2

 

 

 

1/2

0

1/2

 

 

1

0

0

1

 

 

1/6

1/3

1/3

1/6

[D] 四階阮奇庫塔基爾法(Runge-Kutta-Gill Method)

用方塊法表示為

四階阮奇庫塔基爾法

0

0

 

 

 

1/2

1/2

 

 

 

1/2

a

b

 

 

1

0

g

d

 

 

1/6

b/3

d/3

1/6

或寫成

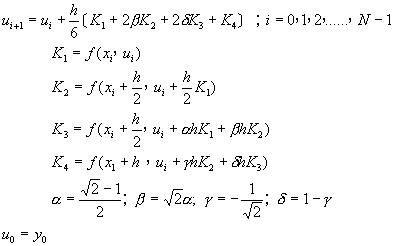         (8-2.16)

[E] 五階阮奇庫塔摩森法(Runge-Kutta-Merson Method)

用方塊法表示為

五階阮奇庫塔摩森法

0

0

 

 

 

 

1/3

1/3

 

 

 

 

1/3

1/6

1/6

 

 

 

1/2

1/8

0

3/8

 

 

1

1/2

0

-3/2

2

 

 

1/6

0

0

2/3

1/6

 

1/10

0

3/10

4/10

2/10

或寫成

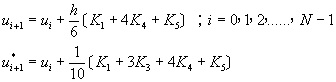                       (8-2.17)

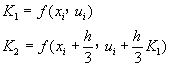
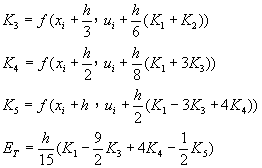
[F] 六階阮奇庫塔布裘法(Runge-Kutta-Butcher Method)

用方塊法表示為

六階阮奇庫塔布裘法

0

0

 

 

 

 

 

1/4

1/4

 

 

 

 

 

1/4

1/8

1/8

 

 

 

 

1/2

0

-1/2

1

 

 

 

3/4

3/16

0

0

9/16

 

 

1

-3/7

2/7

12/7

-12/7

8/7

 

 

7/90

0

32/90

12/90

32/90

7/90

或寫成

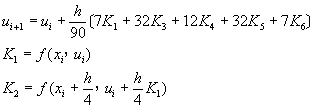                             (8-2.18)

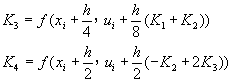
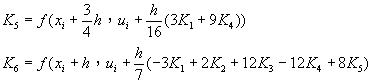
[G] 阮奇庫塔費勃格法(Runge-Kutta-Fehlberg Method)

RKF-1(2)

0

0

 

 

1/2

1/2

 

 

1

1/256

255/256

 

 

1/256

255/256

0

 

1/512

255/256

1/512

 

RKF-2(3)

0

0

 

 

1/4

1/4

 

 

27/40

-189/800

729/800

 

1

214/891

1/33

650/891

 

214/891

1/33

650/891

 

533/2106

0

800/1053

 

RKF-3(4)

0

0

 

 

 

 

2/7

2/7

 

 

 

 

7/15

77/900

343/900

 

 

 

35/36

805/1444

-77175/54872

97125/54872

 

 

1

79/490

0

2175/3626

2166/9065

 

 

79/490

0

2175/3626

2166/9065

 

 

229/1470

0

1125/1813

13718/81585

1/18

 

RKF-4(5)

0

0

 

 

 

 

 

1/4

1/4

 

 

 

 

 

3/8

3/32

9/32

 

 

 

 

12/13

1932/2197

-7200/2197

7296/2197

 

 

 

1

439/216

-8

3680/513

-845/4104

 

 

1/2

-8/27

2

-3544/2565

1859/4104

-11/40

 

 

25/216

0

1408/2565

2197/4104

-1/5

 

 

16/135

0

6656/12825

28561/56430

-9/50

2/55

        RKF-4(5)可以寫成

                           (8-2.19)

其中       

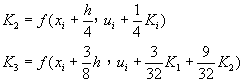
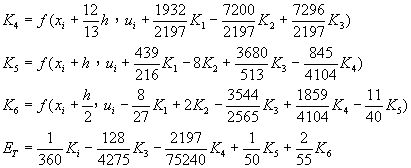
商業化程式名：RKF45, GERK, 本書附有Visual Basic版RKF程式及利用Excel程式的說明，以便讓讀者更了解這種積分方法的應用。

一般而言，利用阮奇庫塔法編寫程式時，可以採用該方法本身估算誤差的功能，編寫成可以自動調節積分間距(Step Size)的程式，以加速積分速度。其策略可以利用以下的Top-Down設計圖表示之。

首先設定一個起始積分間距h

 

計算ui+1及u*i+1

估算誤差Et = ui+1 - u*i+1

推估新的積分間距為

其中 0< p < 1，通常取　p = 0.8

       g = Et的階次

             e = 積分誤差容忍度

　　　　　　　　     If  e > Et

Then                                      Else

淘汰ui+1

接受ui+1

重複計算，直到ui+1被接受

　重複計算到完成積分作業

編寫程式時，同時宜設定h之上限值及下限值，以免e估計不當產生不良結果。積分誤差容忍度最好同時設定絕對誤差及相對誤差。

第三節  聯立微分方程式

高階微分方程式或聯立微分方程式所使用的數值解法與一次微分方程式所使用的方法完全相同。例如要解微分方程式(8-0.1)時，可先將原方程式  I.C.　y(0)＝1，y’(0)＝1        轉換成聯立方程式(8-0.6)的型式

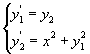        IC　y1(0)＝1，y2(0)＝1                                                (8-0.6)

[A]  四階阮奇庫塔法

將方程式(8-2.14)的四階阮奇庫塔法，延伸成可以解如方程式(8-0.6)的聯立微分方程式，則得到

                                                       (8-3.1)

其中       

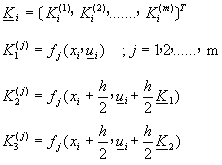
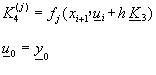
[B]  阮奇庫塔基爾法

用於解聯立微分方程式的阮奇庫塔基爾法為

              (8-3.2)

其中       

               

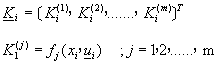
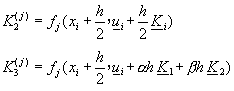
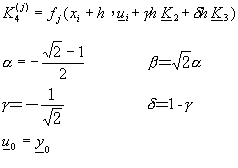
[C]  阮奇庫塔摩森法

用於解聯立微分方程式的阮奇庫塔摩森法為

                            (8-3.3)

其中       

               

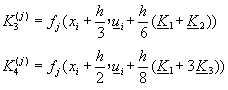
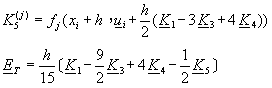
第四節  多間距積分法

阮奇庫塔法(包括低階的歐以勒法)由於只需使用前一間距的計算值，因此，稱為單間距積分法(Single step methods)。這類方法只要有起始條件就可執行下一步驟的計算，而且積分間距可以任意改變，因此，是開始求解微分方程式的最佳工具。但是一旦利用這類方法求得部分資料以後，我們對所積分的函數(及其導函數)事實上已經有了額外的資料，此時如果能夠善用計算機的記憶，利用需要較多資料的多間距積分法，應該可以讓積分效率及穩定性都進一步提昇，當是明智之舉。

多間距積分法的基本原理是利用以前所獲得的y及y’資料建立導函數的近似多項式，並外插至下一積分間距。為了數學處理方便起見，大部分的多間距積分方法都取用等積分間距，主要是讓多項式更易於建立，例如亞當斯法(Adams method)即為典型的例子。使用多間距積分法的時候，所使用的已知數據點點數，會決定所使用多項式的次數，因此，也決定截尾誤差的階次。多間距積分法的階次，等於全部計算誤差中h的羃次，也等於近似多項式的階次加一。

亞當斯法基本上是利用數值積分的原理建立的。首先將微分方程式y’＝f(x，y)由xi積分至xi+1，得到

                                                     (8-4.1)

此方程式的右側積分式中，函數f(x，y)可以利用已知的k個點xi，xi-1，……，xi-k+1，建立一個多項式近似之。若利用牛頓內插法表示f(x，y(x))，則可以得到k間距的亞當斯-貝希佛斯方程式(Adams-Bashforth formula)，其型式為

                                                                         (8-4.2)

其中。若只考慮三個間距的表示式，則(8-4.2)又可以進一步簡化成

                                                     (8-4.3)

利用泰勒級數將及對xi展開，得到

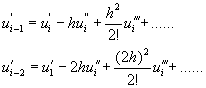
代回方程式(8-4.3)，整理後可以得到

    

                        (8-4.4)

方程式(8-4.4)與ui+1的泰勒級數展開式比較

                                                       (8-4.5)

可以得到b 的聯立方程式

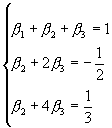
這組線性方程式的解為，及。因此，三階亞當斯—貝希佛斯法可寫成

                                          (8-4.6)

常見的亞當斯法如下表所示：

k

亞當斯貝希佛斯方程式

截尾誤差

1

2

3

4

5

6

多間距積分法使用時，具有無法自動開始啟動運算的困難。習慣上利用兩種方式來克服：

(1) 可以利用同準確度的阮奇庫塔法，建立最初所需資料；然後，再接續使用多間距積分法。

(2) 利用s間距亞當斯法，由s＝1，2，……至s＝k，依序執行。

其中尤其以第(2)種策略的積分效率更佳。利用亞當斯法的積分間距改變策略及程式設計方法請參閱Shampine及Gordon的專書[13]。

例8-2             亞當斯-貝希佛斯法

利用方程式(8-4.6)解微分方程式

        y’＝x＋y﹔IC.　y(0)＝1

假設我們已知y(0.2)及y(0.4)的計算值(可利用阮奇庫塔法求得)，利用積分間距h＝0.2，試求y(0.6)的值。

x

u

u’＝f(x，y)＝x＋u

0

1

1.0

0.2

1.2428

1.4428

0.4

1.5836

1.9836

 

[解]由方程式(8-4.4)

       

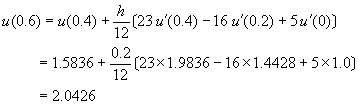
註：理論值2.04424

第五節  亞當斯默頓法

亞當斯貝希佛斯法基本上是利用已知的有限資料，推算下一未知資料的方法，是屬於顯式積分法(Explicit Method)，因此，可以推論其穩定性可能仍然較差。若能使用未知資料與已知資料，一起建立方程式，再利用數學方法求解，以得到下一推估資料，即屬於隱式積分法(Implicit Method)。隱式積分法通常可以克服穩定性問題﹔但一般而言，隱式積分法的程式規劃設計將較為複雜。顯式多間距數值分法由於穩定性差，對於複雜的科學運算，較少被使用。通常，商業化的程式大部分都是利用隱式積分法設計，並且作複雜的積分間距調控處理，以加速積分效率。

隱式多間距積分法的縯導方法與上一節所介紹的方法相當接近，首先將方程式(8-4.2)改寫成

                                                              (8-5.1)

若β0＝0，稱為顯式積分法，若β0≠0則稱為隱式積分法。若α0＝－α1即稱為亞當斯法。顯式亞當斯法稱為亞當斯貝希佛斯法；隱式亞當斯法則稱為亞當斯默頓法。

        考慮k1＝1，k2＝3的亞當斯默頓法，方程式(8-5.1)可以被改寫成

                                            (8-5.2)

仿上一節的縯導方式，將，，，的泰勒級數展開式代入上式中，可以得到

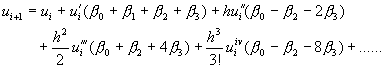              (8-5.3)

此方程式與ui+1的泰勒級數展開方程式比較，

                                           (8-5.4)

可以得到βi的線性聯立方程式為

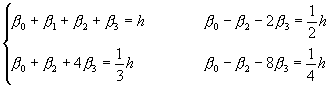
解此聯立方程式，得到

，，，

代回方程式(8-5.2)，即得到亞當斯默頓修正式(Adams-Moulton corrector)為

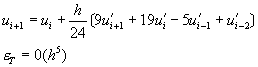                                                (8-5.5)

仿這種方法可以建立不同階次的亞當斯默頓修正式，歸納如下。

k

亞當斯默頓方程式

截尾誤差

1

2

3

4

5

6

        亞當斯默頓法的使用方法，基本上可分成兩大類：

1. 預測修正法:

A. 先利用亞當斯貝希佛斯法做為預測式，利用ui，ui+1，……，ui－k＋1等資料先求出ui+1。

B. 再利用亞當斯默頓法做為修正式，求出更正確的ui+1值。

2. 迭代計算法:

直接利用亞當斯默頓法作計算。由於，因此，方程式(8-5.4)可視為的非線性(或線性)方程式，可利用牛頓迭代法求得。

此外，較著名的商業化程式，包括漢明法(Hamming’s Method)及基爾法(Gear Method)，分別摘要如下：

[A]  漢明法(Hamming’s Method):

                                                         (8-5.6)

商業化程式名：IBM數學副程式HPCG及HPCL。

[B]   基爾法(Gear Method)：

                                                                          (8-5.7)

其中       

               

               

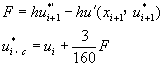
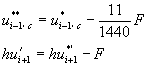
商業化程式名：GEAR，GEARB，EPISODE，EPISODEB

基爾法尤其適用於所謂的「棘手(stiff)」問題。所謂的棘手度(stiffness)是指一組微分方程式的積分困難程度，通常利用方程式Jacobian矩陣的特徵值(Eigenvalue)做判斷。

第六節  特徵值與棘手度

考慮一組聯立方程式

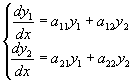　　IC: @ x=0   y1=1   y2=0                          (8-6.1)

其Jacobian矩陣為

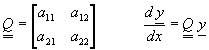                                                          (8-6.2)

Jacobian矩陣的特徵值l為以下方程式的解

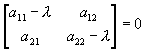                                                                           (8-6.3)

或將此方程式展開成為

定義棘手度(y，Stiffness Ratio)為

                   (8-6.4)

y  < 10                 非棘手的一般問題

y  > 100               棘手的問題

y  > 100000          非常棘手的問題

例8-3             連續反應系統

考慮一連續化學反應，其中反應物Ａ反應生成中間產物Ｂ的反應速率常數為k1=1000，中間產物B反應生成A的反應速率常數為k2=1，中間產物B反應生成產物C的反應速率常數為k3=1。試建立其微分方程式，並判斷此微分方程組的棘手度。

[解] 反應器內的濃度變化可以用以下的聯立方程式表示：

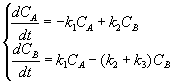  @ t = 0   CA=CA0   CB=0

將濃度CA及CB無因次化，可將原微分方程式改寫成：

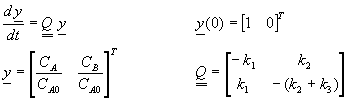
1.                           方程式的理論解為

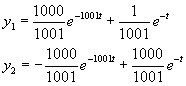
其中y1將非常快速的消耗掉，而y2則需要很長的時間才能完成反應。

2.                           Jacobian矩陣的特徵值

            

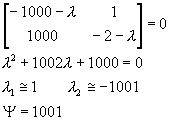
3.                      y  > 100 為一棘手問題。

第七節  隱式阮奇庫塔積分法

阮奇庫塔法為典型的顯式積分法(Explicit method)，因此，可以推論其穩定性可能較差。若使用隱式積分法(Implicit method)則可克服穩定性問題。

顯式阮奇庫塔法(Runge-Kutta Method)的一般式，如本章第二節所介紹，可寫成

                                                                             (8-7.1)

其中為配重因子，n代表所選取xi至xi＋1中的點數，Kj為xi至xi＋1中的某一點的函數f值，

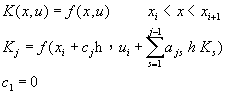                                                      (8-7.2)

隱式阮奇庫塔法則是將方程式(8-7.2)中的Kj表示式修改成隱式表示式：

                                                      (8-7.3)

注意比較方程式(8-7.2)及方程式(8-7.3)，可發現的加總上限由j-1改成j。亦即計算Kj時，也需要Kj本身的資料。因此，才會說將Kj變成隱式表示法。

典型的隱式阮奇庫塔法舉例如下：

一階隱式阮奇庫塔法

1/2

1/2

 

1

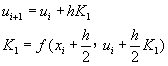                                                                     (8-7.4)

二階隱式阮奇庫塔法

 

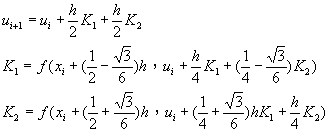                              (8-7.5)

第八節  半隱式阮奇庫塔法

[A] 一階半隱式阮奇庫塔法

考慮一次常微分方程式，其中f(x，y)為x及y的函數。這種函數關係在物理、化學及工程領域中相當常見。如果將此微分方程式作微分，得到

或

       

同理

       

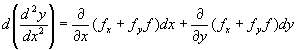
或

       

將微分方程式對(xn,yn)作泰勒級數展開，得到

                                                                                                                     (8-8.1)

首先考慮最簡單的情況，，其中f(y)與x無關。當積分間距小到某一情況時，xn到xn+1間可以看作是一直線，二點間的斜率可以用其中間點的斜率f(yn+1/2)代表。亦即

yn+1 = yn + hf(yn+1/2)                                                                         (8-8.2)

又由常微分方程式，可以得到

                                                                       (8-8.3)

將方程式(8-8.3)代入方程式(8-8.2)中，可以得到

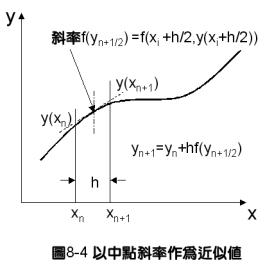
                                                                     (8-8.4)

而由方程式(8-8.1)取到截取誤差為O(h3)，則得到

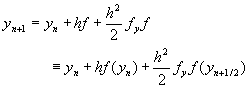                                              (8-8.5)

將方程式(8-8.3)及方程式(8-8.4)代入方程式(8-8.5)中，得到

                                                                              (8-8.6)

代回方程式(8-8.4)，得到

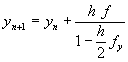                                                                                (8-8.7)

將以上方程式利用泰勒級數展開為，與方程式(8-8.1)比較，其誤差為O(h3)。

將方程式(8-8.7)寫成阮奇庫塔法的方式，可以得到一階半隱式阮奇庫塔法表示式為

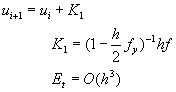                                                                    (8-8.8)

對於M個聯立方程式，其中f(x，y)為x及y的函數，可以仿照方程式(8-8.8)的方式，寫成

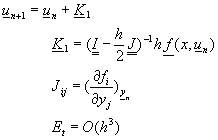                                                         (8-8.9)

[B] 二階半隱式阮奇庫塔法

仿以上的做法，假設考慮最簡單的情況，，且其中f(y)與x無關；利用與上一小節相同的方法，可以擴展到較高階的表示式。將此微分方程式作微分，得到

或

                                                          (8-8.10)

同理

       

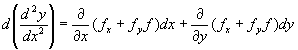
或

                                                                                  (8-8.11)

將微分方程式對(xn , yn)作泰勒級數展開，得到

                   (8-8.12)

假設最簡單的二階半隱式阮奇庫塔法表示式為

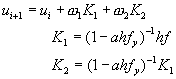                                                              (8-8.13)

將K1及K2的分式展開，得到

                                                      (8-8.14)

                                                  (8-8.15)

代入ui+1的表示式，得到

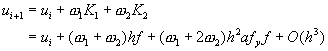                      (8-8.16)

與方程式(8-8.12)比較，得到。解之，得到

                                                             (8-8.17)

為了簡化分析，以取得適當參數，考慮方程式，方程式(8-8.13)可以寫成

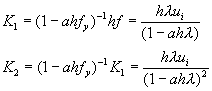
代入方程式(8-8.16)，並作整理，得到

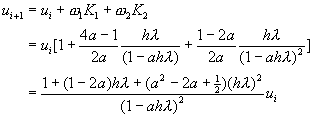                                   (8-8.18)

要提高積分效率，要求在較大時，仍能得到高準確度，可令以上方程式中的項係數為零﹔即，其解為。又當較小時，若也要有良好的積分效率，則所得結果以較佳。因此，代回方程式(8-8.17)，得到

代回方程式 (8-8.13)，得到

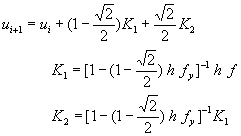                                             (8-8.19)

[C] 羅森布魯克(Rosenbrock)半隱式阮奇庫塔法

羅森布魯克將方程式(8-8.13)寫成一般式

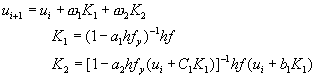                           (8-8.20)

仿上節展開整理後，可得到以下幾種不同結果。

參數

梯形積分法

卡拉漢

羅森布魯克

Trapezoidal

Calahan

Rosenbrock

a1

0.5

0.788 675 134

1-

1.408 248 29

a2

0.5

0.788 675 134

1-

0.591 751 71

b1

0

-1.154 700 540

-1/2

0.173 786 67

c1

0

0

0

0.173 786 67

w1

1.0

0.75

0

-0.413 154 32

w2

0

0.25

1.0

1.413 154 32

Et

O(h3)

O(h4)

O(h3)

O(h4)

[D] 凱勞得半隱式阮奇庫塔法(Caillaud & Padmanabhan)

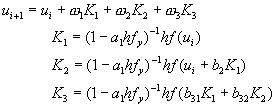                                  (8-8.21)

其中a1為方程式a13 - 3a12 + 3/2 a1 – 1/6 = 0的解。

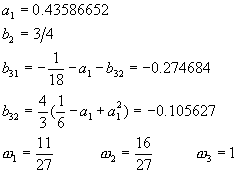
[E] 密齊森半隱式阮奇庫塔法(Michelsen)

密齊森修正方程式(8-8.21)中K3的表示式，得到

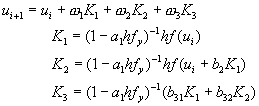                                      (8-8.22)

其中a1為方程式a13 - 3a12 + 3/2 a1 – 1/6 = 0的解。

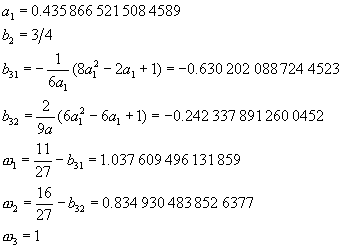                 (8-8.23)

對於M個聯立方程式，其中f(x，y)為x及y的函數﹔密齊森半隱式阮奇庫塔法為一穩定的積分程序，使用上每一積分步驟需要計算一個Jacobian，及計算兩次函數值。可以仿照方程式(8-8.21)的方式，寫成

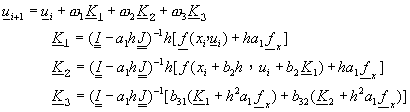       (8-8.24)

其中參數a1，b2，b31，b32，w1，w2均採用方程式(8-8.23)的值。

 

第九節  聯立微分方程式與特徵值

聯立一階微分方程式是工程應用上最常使用的數學模式，由於方程式數目相對較多，不易求得理論解，因此，通常需要利用數值解析的方法求解。考慮N個係數為定值的聯立一階微分方程式

                                                     (8-9.1)

其中矩陣A為(NXN)的方陣，其元素Aij為第i個方程式中yi(t)項的係數。b為常數陣列。當時間t趨近於無窮大時，假設方程式(8-9.1)會得到穩定態的解答。則考慮當時間t趨近於無窮大時，由方程式(8-9.1)可以得到

                                                                                               (8-9.2)

或得到穩定態解答為。由於聯立微分方程式(8-9.1)的解答，可以表示成均勻態方程式的解，再加上特定解。假設方程式的係數矩陣A的所有特徵值都不是零，則均勻態方程式的解答，即為N個均勻態解乘上待定係數ci的總和。待定係數ci則可以利用微分方程式的非均勻邊界條件來決定。

方程式(8-9.1)的均勻微分方程式為，此均勻微分方程式的嘗試解為，代入均勻微分方程式中，可以得到

                                                                      (8-9.3)

或

                                                                                                 (8-9.4)

由本書第四章的說明可知，方程式(8-9.4)為矩陣A的代數特徵值問題，其數值解法詳見本書第四章。方程式(8-9.4)總共可以得到N個不同的特徵值。利用這些特徵值，可以讓均勻微分方程式建立N個獨立的解。利用所求得的均勻解及特別解，可以利用加成原理(Principle of Superposition)得到微分方程式(8-9.1)的完整解答為

                                                                   (8-9.5)

其中待定常數ci可以由t=0時的邊界條件來決定。因此，由方程式(8-9.5)可以得到

                                                                          (8-9.6)

其中U為矩陣A的特徵陣列ui所組成的特徵矩陣。由於矩陣A與特徵矩陣的關係為，由方程式(8-9.6)可以得到待定常數為

                                                                   (8-9.7)

將矩陣A與特徵矩陣的關係式，代回微分方程式(8-9.1)，可以得到

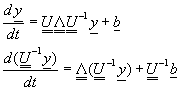                                                                  (8-9.8)

令，則方程式(8-9.8)為陣列Y的一階常微分方程式，解方程式(8-9.8)，可以得到

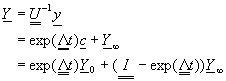                                                      (8-9.9)

或寫成矩陣A及陣列b的函數，為

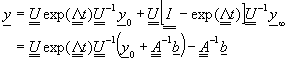                                (8-9.10)

計算策略

利用特徵矩陣求解微分方程式的方法，可以整理如下:

1.      先將所要求解的問題，表示成方程式(8-9.1)的標準形式。

2.      建立矩陣A及陣列b。

3.      求解矩陣A的特徵值，並建立其特徵矩陣U。

4.      利用方程式及，計算。

a.                                        首先將與b乘積放置在陣列w1中﹔

b.                                        再將w1的第i個元素除以特徵值li，放置在陣列w2中﹔

c.                                        然後，計算。

5.      利用方程式(8-9.10)計算y。

a. 首先將與的乘積放置在陣列w3中﹔

b. 再將w3的第i個元素與對角線矩陣相乘，得到第i個元素為，放置在陣列w4中﹔

c. 然後，計算，即為微分方程式的解答。

高階微分方程式的處理策略

係數為常數的M階微分方程式，在引進1至M-1階的導函數作為應變數後，可以轉化成M個一階聯立微分方程式。同理，N個二階聯立方程式，也可以轉化成2N個一階聯立微分方程式。

例8-4             高階聯立微分方程式

試將以下方程式所示之N個二階聯立微分方程式，轉化成聯立一階微分方程式。

                                                                       (8-9.11)

[解] 

首先定義陣列

及

則原方程式(8-9.11)可以寫成

                                                                                 (8-9.12)

                                                                                         (8-9.13)

或整理成

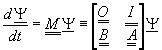                                                                  (8-9.14)

其中M為(2NX2N)的方矩陣。所得到的聯立微分方程式(8-9.14)即可以利用本節所介紹的方法求解。

參考文獻

1.      Caillaud, J. B., and L. Padmanabhan, “An Improved Semi-Implicit Runge Kutta Method for Stiff Systems”, Chem. Eng. J., Vol. 2, pp.227 (1971)

2.      Cocks, A.T., and K.W. Egger, Int. J. Chem. Kinetics., 4, 169 (1972).

3.      Davis, M.E. “Numerical Methods and Modeling for Chemical Engineers”, John Wiley & Sons, New York, (1984).

4.      Forsythe, G. E., M. A. Malcom and C. B. Moler, “Computer Methods for Mathematical Computation”; Prentice Hall, (1977)

5.      Gear, C.W. “Numerical Initial-Value Problems in Ordinary Differential Equations”, Pretice-Hall, Englewood Cliffs, N.J., (1971).

6.     Holland, C.D., and R.G. Anthony, “Fundamentals of Chemical Reaction Engineering” (1987).

7.      Johnston, R. L., “Numerical Method – A Software Approach”, Wiley (1982).

8.      Krogh, F. T., “Algorithms for Changing Step Size”, SIAM J. Numerical Analysis, Vol. 10, pp. 949 (1973).

9.      Michelsen, M. L., “An Efficient General Purpose Method for the Integration of Stiff Ordinary Differential Equations”, AIChE J., Vol. 22, pp.594 (1976).

10.    Michelsen, M. L., “Application of the Semi-Implicit Runge-Kutta Methods for Integration of Ordinary and Partial Differential Equations”, Chem. Eng. J., Vol. 14, pp. 107 (1977).

11.    Robertson, A. H. “Solution of a Set of Reaction Rate Equations” Numerical Analysis, J. Walsh (ed.), Thomson Brook Co., Washington, (1967).

12.    Rosenbrock, H. H. “Some General Implicit Processes for the Numerical Solution of Differential Equations”, Computer J., Vol. 5, pp. 329 (1963).

13.    Shampine, L.F., and M.K. Gordon, “Computer Solution of Ordinary Differential Equations: The Initial Value Problem”, Freeman, San Francisco, (1975).

14.    Villadsen, J., and M.L. Michelsen, “Solution of Differential Equation Models by Polynomial Approximation”, Prentice-Hall, Englewood, Cliffs, N.J., (1978).

 

回首頁     回第三部     下一章