第六章微分與積分

函數的微分與積分是相當重要的數學運算，因此，工程學系的學生在修習微積分學時，都曾花了相當長的時間來學習這類技巧，包括各種函數的微分及積分方法，並學會許多嚴密的證明方法。但是，函數關係如果不是用方程式表示，而是一組f(x)與x的數據來表示，則欲求函數的微分及積分該如何進行呢？在本章中，我們將介紹這類的技巧，並設計所需的計算機程式。本章所介紹的技巧，在第八章以後各章節所探討的微分方程式解法中將極為有用。

在稍後的介紹中，我們將發現數值積分相當容易執行，但是數值微分則需面對較多的困難及危險。這與學微積分時，所感受到微分相當容易，積分相當困難正好相反。

第一節數值微分

在本節中我們將討論利用數值方法計算一階及二階微分的最簡單最直接的方法。在第二節中再討論更一般化的數值微分方法。

假設在x = x₀處，f(x)之導函數定義為

（6-1.1）

因此，若取一相當小的值，則可利用下式得到相當好的近似值。

（6-1.2）

當然，增量可能為正值或負值，因此，亦可用以下的方程式作為近似值。

（6-1.3）

圖6-1中，割線L⁺之斜率等於方程式（6-1.2）的計算值，割線L^-之斜率等於方程式（6-1.3）的計算值。而真正的導函數則等於曲線上處之切線斜率。由圖很清楚地可看出當時，割線L⁺及L^-均會趨近於處之切線。但是由圖6-1，我們可能會推想由P至Q作一直線，所得斜率可能較方程式（6-1.2）及方程式（6-1.3）更接近。

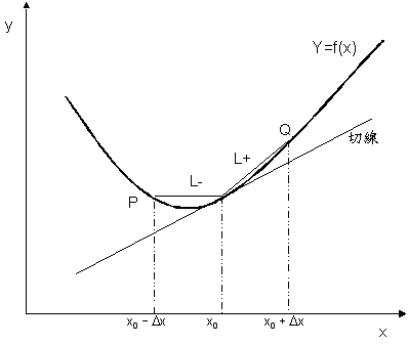
圖6.1 函數f(x)的導函數，有兩種可能的近似值

通過P及Q的直線斜率為

（6-1.4）

正好為方程式（6-1.2）及方程式（6-1.3）所得斜率之平均值。為了方便起見，令，則上式可寫成：

（6-1.5）

我們利用此方程式作為之近似值。

假設我們希望計算f(x)在處的二次導函數。則由方程式（6-1.5），將f(x)代換成得

（6-1.6）

再利用方程式（6-1.5）得一次導函數及分別為

（6-1.7）

（6-1.8）

代入方程式（6-1.6）中，經整理後得之近似值為

（6-1.9）

當然，利用這種方法我們可獲得任何階次的導函數近似值，詳見第三節說明。

第二節微分的計算誤差

本節中將討論利用方程式（6-1.5）及方程式（6-1.9）作一次及二次導函數的近似值時，所引入的截尾誤差（Truncation errors），並探討利用這些近似表示式時所造成的數值計算誤差。

根據泰勒定理，將f(x)對x = x₀展開，得到

（6-2.1）

其中位於及x所界定的封閉區間內。將x用代換，則得

（6-2.2）

其中。同理，利用，得到

（6-2.3）

其中。

將方程式（6-2.2）減去方程式（6-2.3），經整理後得到

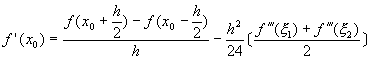（6-2.4）

若為一連續函數，則根據中間值定理（Intermediate Value Theorem）必存在值，使得，且

（6-2.5）

因此，方程式（6-2.4）可以被改寫成

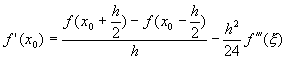（6-2.6）

其中。與方程式（6-1.5）比較，可以得到截尾誤差（真值 - 近似值）為

因此，我們若將間距h減半，則截取誤差可減為倍。理論上，h愈小則結果可能愈佳，但事實上不然。由於計算機的有效位數及準確度問題，當h值小到某一程度以後，由於及變得極為接近，若其差別小於計算機之捨入誤差，則二者的差就機器而言就變成零了，因此，計算結果可能完全錯誤。

相同的分析可適用於二次導函數，仿以上縯導，得到二次導函數表示式（6-1.9）的截尾誤差為

（6-2.8）

注意此截尾誤差亦與成比例，但卻與而非與成比例。

第三節再論數值微分

在本節中，我們將介紹多點微分計算法，以解決例6-1所述之減法消去所產生誤差的難題，並縯導一至四階導函數的一般近似方程式。在本節中，我們將發現計算時，所用點數愈多，則截尾誤差愈小，使我們不必減小h值即可減少截尾誤差，因此，即不必擔心h值過小所產生的問題。

[A] 的三點表示式

首先我們先縯導的三點表示式。假設用於計算的個點為x_-1，x₀及x₁。其中，令

（6-3.1）

（6-3.2）

其中，。則我們可仿照方程式（6-1.5）的型式，將表示成為、及之線性函數

（6-3.3）

我們希望決定最佳的，及值。首先考慮當f(x) = 1時，我們當然希望方程式（6-3.3）完全正確，此時，因此，由方程式(6-3.3)可以得到

（6-3.4）

其次考慮當時，也希望方程式（6-3.3）為完全正確，此時，故由方程式（6-3.3）可以得到

（6-3.5）

最後考慮當時，希望方程式（6-3.3）也能滿足此拋物線方程式。此時，由方程式（6-3.3）可以得到

（6-3.6）

係數，及必須滿足聯立方程式（6-3.4），（6-3.5）及（6-3.6）。其解為

（6-3.7）

（6-3.8）

（6-3.9）

需注意因為，，因此上列諸式必然存在。代回方程式（6-3.3），得到一次導函數的一般表示式為

（6-3.10）

[B] 微分的五點表示式

其次再考慮五點的表示式。假設此五點分別為，，，及，其中，。利用這五點的函數值f(x)求取之近似值，仿以上處理方式，將寫成五個函數值的線性組合：

（6-3.11）

我們希望找出，，，及的值。

如前述，令f(x) = 1，即，則由方程式（6-3.11）可以得到

（6-3.12）

其次，令，即；由方程式（6-3.11）得到

（6-3.13）

又令，得到

（6-3.14）

令，得到

（6-3.15）

最後令，得到

（6-3.16）

方程式（6-3.12）至（6-3.16）計有五個方程式，並含五個未知數，，，及。其解較為繁複，為了簡化分析起見，假設，，且，則可以得到

故方程式（6-3.11）變成

（6-3.17）

此表示式對任何四次以下的多項式均為正確表示式。

同理，我們可以證明二次、三次及四次導函數導的等間距五點表示式分別為

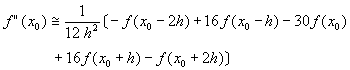（6-3.18）

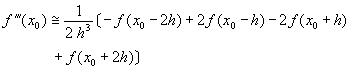（6-3.19）

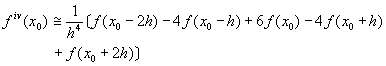（6-3.20）

這種縯導相當簡單，對於更高階次的微分或更多點的近似表示式均可仿以上步驟縯導之。請注意以上的導函數近似表示式的係數和都等於零，因此，如果h值相當小時，都會產生減法消去所造成的嚴重錯誤，使用時必須特別謹慎。

應用本節所介紹差分法解微分方程式的方法，詳見第九章及第十一章。

第四節數值積分

在以下各節中，我們將介紹三種常用的數值積分方法，分別建立Visual Basic程式，並比較其執行效率。考慮函數f(x)之定積分式

（6-4.1）

方程式(6-4.1)的計算值，可解釋為在[a，b]區間內，在函數f(x)曲線下之面積，如圖6.2所示。積分式的計算對某些函數而言可能相當簡單，可是有時候也有可能相當複雜，或無法直接積分，而必須藉助於適當的近似方法，即數值積分（Numerical integration）。

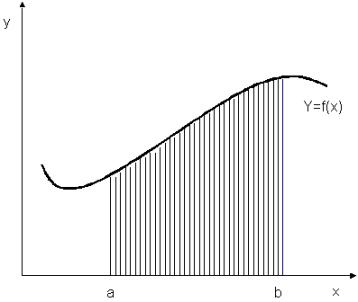
圖6.2 函數f(x)之定積分

常用的數值積分方法通常是將原函數f(x)用一易於積分的函數取代，這種新函數可能為一多項式，如直線、拋物線、或是超越函數，如正弦函數或餘弦函數等。數值積分計算結果的準確性就決定於替代函數與原函數的近似程度。

下一節中，我們首先介紹梯形積分法，並利用此方法介紹函數替代的原理。

第五節梯形積分法

梯形積分法是所有數值積分法中最簡單的一種。這種方法基本上是利用一組直線線段來替代原函數。將積分範圍分割成n個等間距的子區間，其寬度為

（6-5.1）

其中n為子區間數，b及a分別為積分式的上下限。首先考慮只有單一子區間的情況，如圖6.3所示，若整個區間用單一直線作為原函數之近似，則所求得面積為

（6-5.2）

在此式中，f(a)為積分式下限處的函數值，f(b)為積分式上限處的函數值。

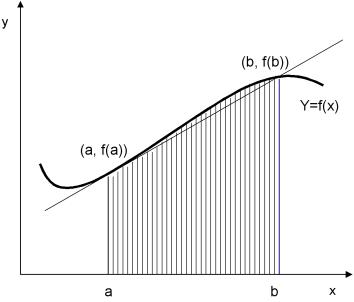
圖6.3 單一子區間之梯形積分

對於更一般化的情況，若將整個區間[a，b]分成n個子區間，則第i + 1個子區間的積分上下限分別為及，如圖6.4所示。在每一子區間上的函數曲線分別用一直線方程式取代，由於每一子區間的形狀均成梯形，故稱為「梯形積分法」。

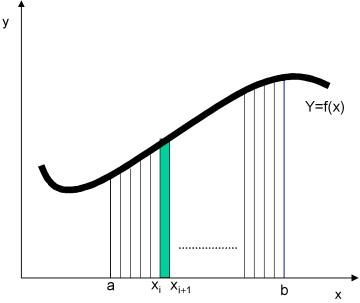
圖6.4 n個子區間之梯形積分

利用梯形積分法時，第i + 1個子區間的面積為

（6-5.3）

其中，，i = 0，1，2，……，分別為第i + 1個子區間之左側及右側函數值。我們所要求解的積分式（6-4.1）即為各個子區間面積的總和：

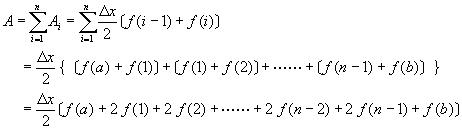
（6-5.4）

利用梯形積分法所造成的截尾誤差，等於函數區間y = f(x)與(x_i，f(x_i))及(x_i+1，f(x_i+1))所形成的弦之間的扇形區域面積和。當子區間的數目愈大，則此扇形面積和愈小，即截尾誤差愈小。考慮函數y = f(x)對x = x_i點之泰勒級數展開式：

（6-5.5）

同理，對x = x_i+1點作泰勒級數展開為

（6-5.6）

以上二方程式雖然都是正確的，但卻無法用於和方程式（6-5.4）作比較。因此，首先取上二式的平均值，得到

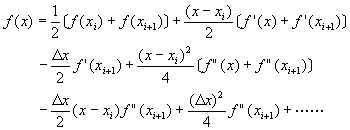（6-5.7）

將f(x)dx由x_i積分至x_i+1，並以f(i)代表f(x_i)，得到

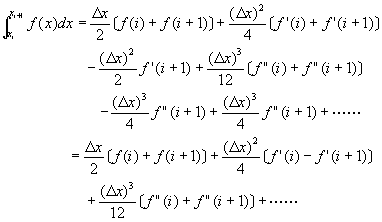（6-5.8）

此方程式為第i + 1個子區間之真正積分近似值，與方程式（6-5.3）比較，顯示梯形積分法將以上諸項捨去。因此，梯形積分法之截尾誤差為

（6-5.9）

當非常小時，上式可用第一項近似之。由於利用泰勒級數展開，並乘以，可以得到

（6-5.10）

表示與方程式（6-5.9）的第一項仍呈某種比例關係，依此類推，較高次項亦與第一項成某種比例關係。故可將梯形積分法的截尾誤差寫成

（6-5.11）

其中K為一未定係數。在此假設K大約成一定值。

考慮函數f(x) = x²。則代入積分式中，可以得到

（6-5.12）

而由方程式（6-5.8）則得到

（6-5.13）

令方程式（6-5.12）與方程式（6-5.13）兩式相等，則得到

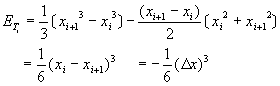（6-5.14）

與截尾誤差的一般式方程式（6-5.11）比較，得到

（6-5.15）

即

（6-5.16）

由於總截尾誤差為各個子區間截尾誤差之和，故得

（6-5.17）

第六節理查遜展延法

梯形積分法為一相當簡單的數值積分法，最大缺點是計算時需分割成相當多的子值間進行積分，才能獲得滿意的準確度。因此，本節將介紹一種簡單的改良方法，以提高其準確度。

梯形積分法的截尾誤差（Truncation error）如方程式（6-5.17）所示，與子區間寬度的平方成正比，因此，可以表示成：

（6-6.1）

其中截尾誤差比率係數a的表示式為

（6-6.2）

由於f’(a)及f’(b)並不明確，但假設a約成定值，則可以利用以下做法推估之。首先，令I_h為時利用梯形積分法所得到的結果，I_k為時利用梯形積分法所得到的結果；由於積分截尾誤差可以用方程式(6-6.1)表示，因此，真正的積分值I分別可以寫成

（6-6.3）

（6-6.4）

將所得到的兩個方程式相減，整理得到截尾誤差比率係數a的表示式為

（6-6.5）

將此結果代入方程式(6-6.3)，可以得到

（6-6.6）

利用這種方法可以求得比I_h及I_k更好的近似值。這種方法稱為理查遜展延法(Richardson’s Deferred Approach)。使用上，通常以半間距作展延，即k=h/2。

第七節辛普森積分法

辛普森積分法是最廣泛被使用的數值積分法，基本上與梯形積分法相似，都需要將積分的範圍分割成許多的小區間，然後計算在各子區間端點處的函數值。辛普森積分法與梯形積分法比較，唯一的區別在於函數曲線下面積的近似方法不同。梯形積分法是將子區間的面積用一梯形作近似，辛普森法則是將兩個相臨的子區間的函數曲線用一拋物線作近似。因此，梯形積分法只在函數為一次多項式時為正確，而辛普森法則在函數為三次或三次以下的多項式時均為正確。故辛普森積分法是一種計算方法與梯形積分法相仿，但準確度較高的數值積分方法。

以下我們根據梯形積分法及前節所介紹的理查遜展延法來縯導辛普森積分方程式。在梯形積分法中，假設子區間的數目為

（6-7.1）

假設n為偶數，並令

（6-7.2）

則由梯形積分法方程式（6-5.4）得到

（6-7.3）

（6-7.4）

將方程式（6-7.2）、方程式（6-7.3）及方程式（6-7.4）代入理查遜展延法之方程式（6-6.6）中，可以得到

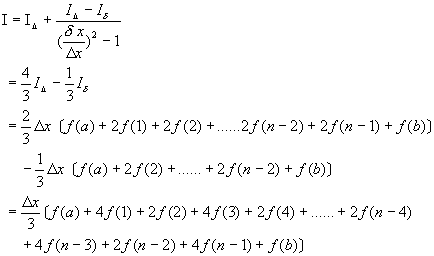（6-7.5）

方程式（6-7.5）即稱為辛普森積分法則（Simpson’s Rule）。其截尾誤差為

（6-7.6）

辛普森法的截尾誤差與子區間寬度的四次方成正比，而梯形積分法則與成正比。

辛普森積分法程式設計時，亦可仿梯形積分法作端點校正誤差。如方程式（6-7.6）所示，利用辛普森法端點校正需使用函數的四次導函數，而本章稍前曾談及方程式之數值微分常會引入較大的誤差，因此，就程式設計及應用目的而言，端點校正最好只用一次導函數。含一次端點校正誤差的辛普森積分法則為：

i為偶數，j為奇數（6-7.7）

第八節龍勃格積分法

利用梯形積分法計算以下的積分式時

（6-8.1）

若只取一個區間，則得到

（6-8.2）

若將積分範圍分成兩個子區間，即，則得到

（6-8.3）

同理，取四個子區間時，，得到

依此類推得到當﹔子區間數為個時

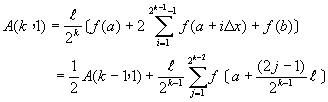（6-8.4）

在以上諸方程式中，積分近似值A（I，J）的I表示子區間數為，J = 1表積分時利用線性函數取代原函數f(x)。

仿以上的處理方式，若利用拋物線方程式取代原函數f(x)，即利用辛普森積分法，可得﹔子區間數為

（6-8.5）

比較方程式（6-8.4）及方程式（6-8.5），得到梯形積分法與辛普森積分法之關係為

（6-8.6）

同理類推得m次曲線近似值方法所得結果為

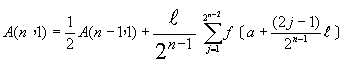（6-8.7）

（6-8.8）

我們利用這種外插法可很快地得到收斂的正確積分值。這種方法即稱為龍勃格積分法，事實上，這種方法與理查遜展延法完全相同。實際計算時，只需先求出梯形積分法所得的結果A(I，1)，然後利用（6-8.8）外插即可求得正確的結果。

第九節高斯積分法

以上各節所介紹的數值積分法，使用者通常可隨意地自行選擇子區間寬度。而在實際使用上，我們通常選用相同的。假使我們放棄這種自由選擇子區間寬度的權利，而利用精確的子區間最佳決定策略，理論上應該可以獲得較高準確度的回報，高斯積分法（Gauss Quadrature）就是這類方法中的一個典型的例子。

試回想前述三種積分方法：梯形積分法、辛普森積分法及龍勃格積分法，基本上均可將這些積分方法寫成

(6-9.1)

其中稱為配重係數，則是在x = x_i處的函數值。例如，辛普森法中，，。

為了方便處理起見，如果將積分式的上下限利用變數轉換，使上下限變成0與1：

(6-9.2)

則方程式(6-9.1)可以被轉換成以下的積分型式，

(6-9.3)

假設函數f(x)可以用一個多項式表示，並令，則可以將函數f(x)寫成

(6-9.4)

由於

(6-9.5)

而又由方程式(6-9.3)得到

(6-9.6)

定義，則由方程式(6-9.5)及方程式(6-9.6)相等，可以得到

(6-9.7)

或改寫成矩陣型式為

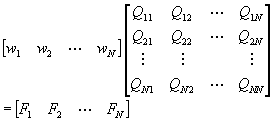(6-9.8)

(6-9.9)

由於及，由方程式(6-9.9)直接可以求解配重係數矩陣的關係式為：

(6-9.10)

計算策略：

1. 決定配置點數目N。

2. 決定需要求解的未知數數目m，未知數包括：配置點x_i及配重係數w_j。

3. 利用方程式(6-9.6)建立未知數的關係式。其中基礎函數的最大i值，等於m。

4. 由以上所建立的關係式，求得配置點x_i及配重係數w_j。

5. 利用方程式(6-9.3)求得函數f(x)的積分值。

例6-5 高斯積分法

利用高斯積分法時，若採用N=3，試求配重係數為何。

[解]

(1) 當N=3時，總共需要求解的未知數包括：

配置點： x₁，x₂，及x₃

配重係數： w₁，w₂，及w₃

亦即需要求解六個未知數。為了方便說明起見，假設x₁=0，x₃=1，則未知數只剩下四個，要解四個未知數需要有四組方程式，即N=4，亦即，函數積分可以準確到x³項。若假設f(x) = f₁ = 1，則方程式(6-9.3)必須仍能成立，亦即

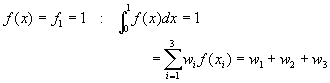
同理，若令f(x) = f₂ = x，f(x) = f₃ = x²，f(x) = f₄ = x³，則方程式(6-9.3)也必須都能成立，亦即

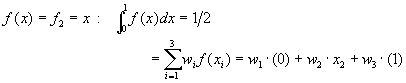
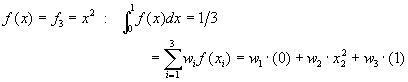
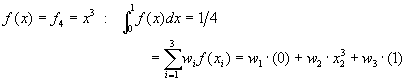
在以上的演導中，選擇x₁=0，x₃=1，x₂為未知的配置點，加上配重係數w₁，w₂，及w₃，我們總計有四個未知數及四組方程式，

以上四組方程式的解為x₂=1/2，w₁=1/6，w₂=2/3，w₃=1/6，結果與辛普森法完全相同，可將積分式寫成

(2) 若不假設x₁=0，x₃=1時，總共需要求解的未知數包括：

配置點： x₁，x₂，及x₃

配重係數： w₁，w₂，及w₃

亦即需要求解六個未知數。要解六個未知數需要有六組方程式，即N=6，亦即，函數積分可以準確到x⁵項。仿上演導，可以得到下列方程式：

以上方程式的解為

x₁=0.112 701 6654

x₂=0.500 000 0000

x₃=0.887 298 3346

w₁=0.277 777 7778

w₂=0.444 444 4444

w₃=0.277 777 7778

利用方程式(6-9.10)求解配重係數w時，必須先知道配置點x，而由以上簡單的實例，我們可以發現如果利用f_i(x) = x^i-1代入方程式(6-9.3)，聯立求解x及w，會得到一組非線性聯立方程式，其求解過程將變得相對複雜。但如果使用雅可必(Jacobi)多項式之類的正交多項式(Orthogonal Polynomial)來代替f_i，並以n次正交多項式的根作為配置點，則可輕易的求得配重係數w。有關配置點及配重係數相關問題，請閱讀本書第十章數學配置法，有更詳細的討論及說明。

第十節高斯-雅可必積分法

高斯-雅可必積分法(Gauss-Jacobi Quadrature)是利用正交多項式之一的雅可必多項式(Jacobi polynomial)取代高斯積分法中的基礎函數f_i(x)= x^i-1，並利用雅可必多項式的根作為配置點，以簡化求解配重係數的方法。

表6-10.1 典型的雅可必多項式

		N=0	N=1	N=2	N=3
0	0	1	2x-1
1	0	1	3x-1
2	0	1	4x-1
0	1	1
1	1	1	2x-1
2	1	1

表6-10.2 正交多項式()的根及方程式(6-9.3)所定義的配重係數

N
1	0.50000 00000	0.66666 66667
2	0.21132 48654 0.78867 51346	0.50000 00000 0.50000 00000
3	0.11270 16654 0.50000 00000 0.88729 83346	0.27777 77778 0.44444 44444 0.27777 77778
4	0.06943 18442 0.33000 94783 0.66999 05218 0.93056 81558	0.17392 74226 0.32607 25774 0.32607 25774 0.17392 74226
5	0.04691 00771 0.23076 53450 0.50000 00000 0.76923 46551 0.95308 99230	0.11846 34425 0.23931 43353 0.28444 44444 0.23931 43353 0.11846 34425
6	0.03376 52429 0.16939 53086 0.38069 04070 0.61930 95931 0.83060 46933 0.96623 47571	0.08566 22462 0.18038 07865 0.23395 69678 0.23395 69678 0.18038 07865 0.08566 22462
註： (1) 上列雅可必方程式中，假設。 (2) 配置點為x₁=0，x_N+2=1，其他x₂，x₃，…，x_N+1如上表所列。 (3) N=1時，w₁=w₃=1/6，w₂=2/3。 (4) N>2時，w₁=w_N+2=0。