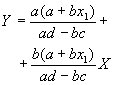回首頁     回第二部     到第三部

第七章  實驗數據分析

工程科學是一門由經驗累積，並且相當仰賴實驗數據的科學，因此，有非常多的研究人員窮畢生精力進行各種領域的實驗工作，各種實驗數據也不斷地累積，以驗證理論及建立經驗方程式。而在實際應用時，零亂未經整理的數據，在應用上相當困難，並且沒有價值；有效率且規律性的實驗數據整理與處理，對工程及科學而言是相當重要的。實驗數據的整理與處理，通常必須兼顧基本原理的正確性及使用時的正確性與方便性。一般而言，實驗數據資料處理通常使用以下三種方法：

(1)    表格表示法：例如空氣比熱Cp與溫度及壓力的關係，如表7.1所示；希望求得某一溫度、壓力時的Cp值，可利用本書第三章所介紹的插值法求之。

表7.1  空氣之比熱 Cp (J/mole-K)

T(K)

P(atm)

1

10

20

30

180

29.52

31.24

33.51

36.14

200

29.38

30.59

32.10

33.73

220

29.26

30.14

31.23

32.38

240

29.16

29.88

30.72

31.60

(2)    圖形表示法：將函數關係製作成圖形，使用時再按圖索驥，由圖讀取函數值。這種方法最大的缺點是讀數據時準確度較差。

(3)    函數近似法：將實驗所得數據利用一經驗方程式表示。經驗方程式的建立，通常需仰賴圖形表示法先建立大略的函數關係，或佐以理論基礎，再判斷可使用的函數型態，然後以數學方法建立經驗式。

本章將利用實際數據的處理來介紹(2)及(3)兩種使用方法。

第一節  圖形分析法

實驗所得原始數據，有時看似雜亂無章，但如果先作適當處理，然後再作圖，則很可能使原先看似不規則的實驗數據，顯現出規則的函數關係。這種實驗數據的處理，通常需建立在對該一現象或觀察的理論分析上﹔但對於一項嶄新的實驗觀察，有時也可能由實驗結果分析及各種歸納，引導出新理論的建立。

以表7.2的數據為例，直接作圖，可以得到如圖7.1所示之曲線關係。

表7.2   典型的數據表

x

y

x/y

0.00

0.00

-

0.50

1.00

0.50

1.21

1.50

0.81

3.10

1.92

1.61

4.17

2.01

2.07

4.98

2.05

2.43

5.77

2.09

2.76

9.00

2.17

4.15

12.10

2.21

5.48

17.00

2.24

7.59

 

 

 

 

 

 

 

 

 

但若先計算x/y值，再以(x/y)對x作圖，則可以得到如圖7.2所示的直線關係。以方程式表示之，得到

                                                                           (7-1.1)

其中m為圖7.2所示直線的斜率，b為截距。移項整理後，得到y與x的函數關係為

                                                                                             (7-1.2)

工程上常用的作圖格式，包括正交作圖、半對數作圖、全對數作圖及或然率作圖等，分別有其使用上的特色與用途。以下分0別就各種函數型式的適當作圖方法作一簡要說明。

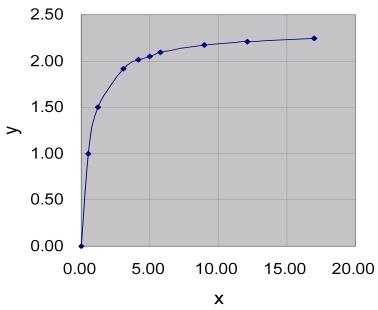
圖7.1  y對x作圖

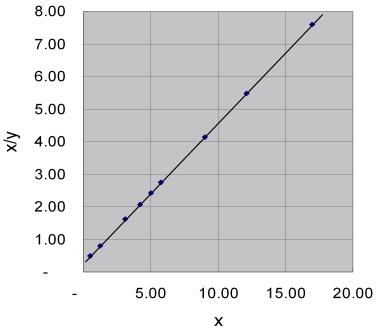
圖7.2  x/y對x作圖，成一直線關係

 

[a]

要將這類函數轉換成直線關係，可對原方程式左右同時取對數，得到

                                                            (7-1.3)

此時，若令Y=Log y， X=Log x，則上式可改寫成

Y = a + n X                                                                                              (7-1.4)

為一直線方程式，如圖7.3所示，利用全對數座標製作Y對X的圖形，可以得到直線關係。

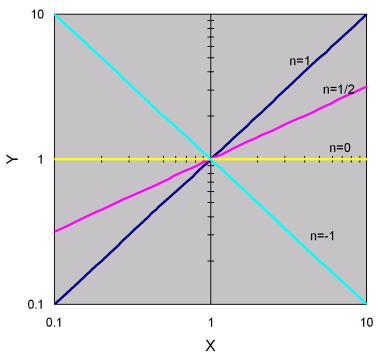
圖7.3  函數， m=1

工程上常用對數座標紙，將數據直接繪製於圖紙上，若所得結果呈現類似圖7.3的線性關係，則可推斷原始數據可利用函數關係表示。

[b]

這類型的函數曲線如圖7.4所示，其特點為：

1.     一定通過（0，1）這一點。

2.     若m＞0，則當x增大，y會趨近於無窮大﹔但若m＜0，則當x增大，y會趨近於0。

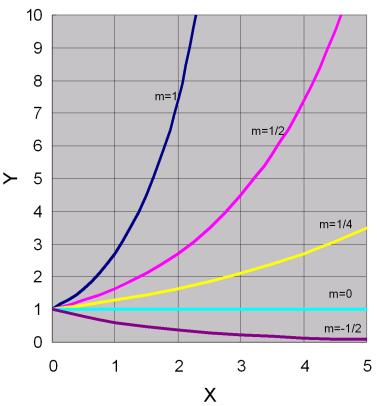
圖7.4 

要將此方程式轉換成直線關係，同樣可對原方程式取對數，得

（log y）＝mx                                                                                      (7-1.5)

令Y＝log y，X＝x，則Y對X作圖為一通過原點的直線。圖7.5即函數利用半對數紙作圖所得結果，原方程式可被轉換成線性關係。

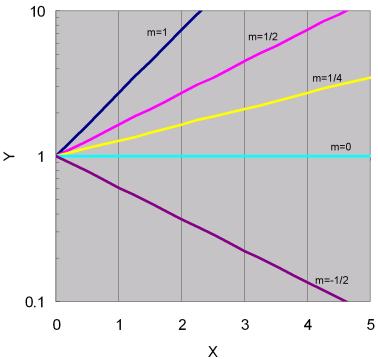
圖7.5  函數

[c]

此類型的函數曲線如圖7.6所示，其特點為：

1.    一定通過原點（0，0）。

2.    當x增大時，y會趨近於1。

3.    c值愈大，y趨近於極限值1的速率即愈快。

這類函數常見於反應速率表示式。轉換成線性關係式的方法，可利用下列二種方式：

a.     若將函數作適當轉換，令Y＝1／y，X＝1／x，則原方程式可改寫成

                                                                                        (7-1.6)

        所得到直線圖形如圖7.7所示。當x趨近無限大時，1/x趨近於零，y值趨近於1。當參數c趨近於無限大時，x值變化之影響即變得不明顯，y值趨近於1。

b.     若將函數作適當轉換，令Y＝x／y，X＝x，則原方程式可改寫成：

                                                                                          (7-1.7)

        直線圖形如圖7.8所示，斜線均為1，截距則隨c值而變。c值趨近於無窮大時，所得直線位於圖形對角線上，即Y=X。

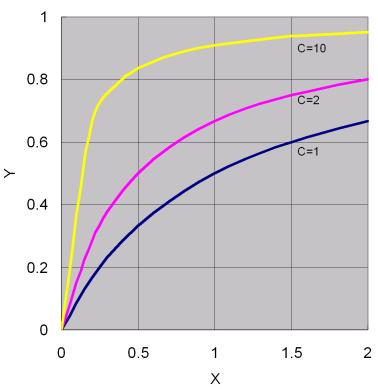
圖7.6  函數

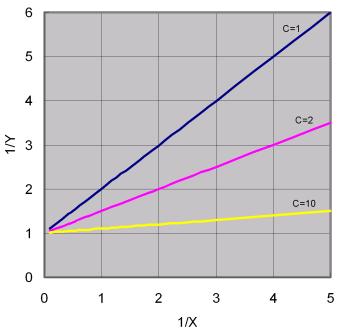
圖7.7  函數之轉換

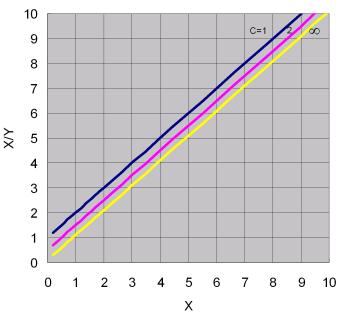
圖7.8　函數之轉換

 

例7-1             氣體狀態方程式係數推定

已知苯蒸氣在290℃時的莫耳體積如表7.3所示。假設苯蒸氣的P-V-T關係可利用維瑞耳狀態方程式（Virial Equation of State）表示：

                                                                             (7-1.8)

試求係數及值。

表7.3  苯蒸氣在290℃時的莫耳體積

P (atm)

V (cm3/mole)

P (atm)

V (cm3/mole)

30.64

1,114

40.04

707

31.60

1,067

41.79

646

32.60

1,013

43.59

591

33.89

956

45.48

506

35.17

900

47.07

443

36.63

842

48.07

386

38.39

771

 

 

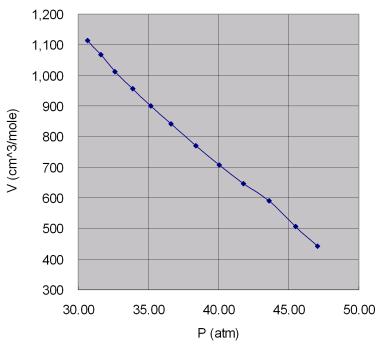
圖7.9　苯蒸氣的莫耳體積與壓力關係圖

[解]

將原始數據（P，V）作圖，得一略呈S型的曲線，如圖7.9所示。尤其當壓力P增大時，其線性關係有較明顯變化。

維瑞耳狀態方程式可改寫成線性函數：

                                                                    (7-1.9)

令，，則原方程式可改寫成

                                                                                       (7-1.10)

為一直線，由其斜率及截距即可分別求得及。

圖7.10即為對 [1／V] 作圖所得結果，由圖得斜率＝3.53×104，截距＝－323。

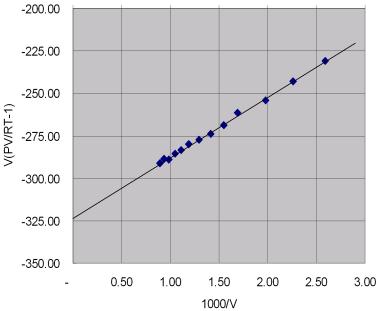
圖7.10　維瑞耳狀態方程式之線性化

第二節  最小平方法

前一節簡單的介紹了幾種函數的線性化方法，可是如例7-1所示，數據利用適當轉換後，雖然可以變成直線關係，但要如何在所繪製的數據點之間劃一條最具代表性的直線呢？「最佳近似」直線的定義有許多種不同的說法，其中最常見也被使用得最廣泛的，就是能使所有的數據點與近似方程式誤差的平方和為最小的直線，這種方法即稱為「最小平方法」（Least Square Method）。

假設實驗所得數據為（xi，yi），i＝1，2，……，n。令所有數據點的「最佳近似」直線為

                                                                                    （7-2.1）

此直線與n個數據點誤差（近似值與實側值之差）之平方和為：

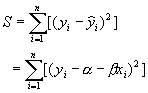                                                                  （7-2.2）

要求得最佳係數及，使誤差的平方和S變成最小，則需滿足以下二條件:

                                      （7-2.3）

                                （7-2.4）

方程式(7-2.3)及方程式(7-2.4)展開後，可分別改寫成

                                                             （7-2.5）

                                                   （7-2.6）

得到二聯立方程式，求解兩個未知變數及。解以上二聯立方程式，得到及分別為：

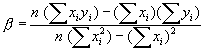                                                   （7-2.7）

                                                                 （7-2.8）

例7.2  最小平方法

利用本節所介紹的最小平方法，試求例7.1中的係數及值。

[解] 維里狀態方程式可改寫成線性函數：

                                                                  (7-2.9)

令，，則原始數據可整理如表7.4。

表7.4  苯蒸氣在290℃時的莫耳體積

P(atm)

V(cm3/mole)

X=1/V

30.64

1,114

8.98E-04

-291.14

31.60

1,067

9.37E-04

-288.46

32.60

1,013

9.87E-04

-289.06

33.89

956

1.05E-03

-285.73

35.17

900

1.11E-03

-283.51

36.63

842

1.19E-03

-280.01

38.39

771

1.30E-03

-277.15

40.04

707

1.41E-03

-273.89

41.79

646

1.55E-03

-268.60

43.59

591

1.69E-03

-261.52

45.48

506

1.98E-03

-254.01

47.07

443

2.26E-03

-243.10

48.07

386

2.59E-03

-231.01

然後分別求得，，，為

代入方程式(7-2.7)及方程式(7-2.8)，即可得到

這種計算利用Excel撰寫程式最為簡單，利用Excel所建立表格如表7.5所示，詳細程式編寫方法，可參考所附光碟。

表7.5  利用Excel計算例7.2之結果

N

X

Y

X^2

XY

1/V

V*(PV/RT-1)

(1/V)^2

(1/V)*(V*(PV/RT-1))

1

8.98E-04

-291.18

8.06E-07

-2.61E-01

2

9.37E-04

-288.50

8.78E-07

-2.70E-01

3

9.87E-04

-289.10

9.74E-07

-2.85E-01

4

1.05E-03

-285.76

1.09E-06

-2.99E-01

5

1.11E-03

-283.54

1.23E-06

-3.15E-01

6

1.19E-03

-280.04

1.41E-06

-3.33E-01

7

1.30E-03

-277.18

1.68E-06

-3.60E-01

8

1.41E-03

-273.91

2.00E-06

-3.87E-01

9

1.55E-03

-268.62

2.40E-06

-4.16E-01

10

1.69E-03

-261.54

2.86E-06

-4.43E-01

11

1.98E-03

-254.02

3.91E-06

-5.02E-01

12

2.26E-03

-243.11

5.10E-06

-5.49E-01

13

2.59E-03

-231.01

6.71E-06

-5.98E-01

SUM

1.89E-02

-3.53E+03

3.11E-05

-5.02E+00

=(N*SUM(XY)-(SUM(X)*SUM(Y))/((N*SUM(X^2)-(SUM(X))^2))

=35,277.51

=(SUM(Y)-Beta*SUM(X))/N

=-322.7499694

 

函數關係的選擇並非完全沒有規則可依循，對所觀察現象或所量測對象的基本原理之了解，通常有助於建立函數關係。但如本章第一節所討論，實驗數據並不一定都會成線性關係，因此，我們可能時常需面對選擇近似方程式的難題。

若將實驗數據描繪在方格紙上，或用Excel軟體嘗試將實驗數據作圖，通常有助於由曲線的形狀及對實驗性質的了解，提出可代表這些數據的方程式。而所提出方程式的適用性，最簡單而有效率的檢查方式，就是先將方程式轉換成線性關係，並作圖判斷數據與方程式的一致性。表7.5為一些常見的單變數函數的線性轉換法。利用這種轉換技巧，即可將非線性函數轉換成線性函數，然後再利用本節所介紹的最小平方法推定其係數。

表7.5  單變數函數的線性轉換

原方程式

直線轉換座標

直線方程式

漸近線及備註

X座標

Y座標

x

1/y

1/x

Y

x

x/y

1/x

1/y

 

x

(x1,y1)為一數據點

log(x)

log(y)

log(x)

log(y-)

之近似值

可利用xà0求之

x

log(y)

通過(0,)

第三節  非線性函數近似法

上一節中，我們介紹許多種函數線性化的策略，但除了表7.5所示的非線性方程式以外，多項式方程式也是一種常被使用的近似方程式。尤其是要對所獲得的近似方程式作微分或積分運算時，多項式更是易於使用。

由於多項式運算容易，因此，作圖結果如果不是直線的函數，即可考慮利用多項式方程式來表示。事實上，我們常用的物理化學性質資料如熱容量Cp及黏度等，通常就是利用多項式做為近似表示式。

利用多項式函數做為數據點之最佳近似，其處理策略與上一節所介紹的最小平方法相同。假設多項式近似函數為

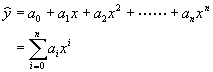                                                         (7-3.1)

定義實驗數據與近似式的誤差為

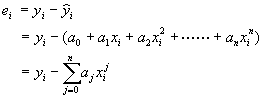                                             (7-3.2)

上式中，為實驗值，表示近似值﹔為自變數，且假設沒有測量誤差。我們希望使誤差的平方和達到最小，

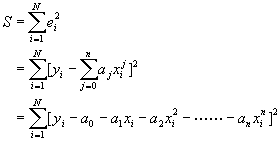                                          (7-3.3)

其中n為多項式的階次，N為數據點的總數目。

當S值達到最小的時候，所有參數ai對S的偏微分應該都等於零。亦即，可建立n+1個方程式：

 

將各方程式除以(-2)，展開得到n+1個聯立方程式：

*       

                 (7-3.4)

將上列聯立方程式寫成矩陣型式，得

                                                                                     (7-3.5)

其中

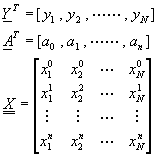                                                                       (7-3.6)

方程式(7-3.4)可以利用本書第四章所介紹的高斯消去法求解向量A，再代回方程式(7-3.1)，即可得到所需要的近似方程式。

第四節  多變數線性迴歸

實驗數據時常會含有兩個以上的變數。例如氫氣與氮氣經催化生成氨的反應常數Kp，即決定於反應溫度T及壓力P，亦即Kp＝f（T，P）。其次，如流體在管中流動的對流熱傳係數與流體流速、物性及管徑有關，利用因次分析可得到以下的關係式：

        Nu＝f（Re，Pr）

其中Nu＝hD／k ，Re＝DUρ／μ，Pr＝ρCpμ／k，h為熱傳係數，D為管子的直徑，k為流體的熱傳導係數，ρ為流體密度，μ為流體的黏度，Cp為流體的熱容量，U為流體的平均流速。

        因此，在分析實驗數據時，時常需將一變數寫成其他變數的函數，如

        v＝f（x1，x2，……，xm）                                                            （7-4.1）

在本節中，我們將只線討論線性模式的迴歸分析，其他型式如多項式、指數函數、三角函數等亦可利用相似的方法處理之。假設函數f為xi，i＝1，2，……，m的線性函數，則方程式（7-4.1）可改寫成

        ；x0＝1                      （7-4.2）

其中為模式推定值。線性模式推定值與實驗測量值y的誤差為

        ；j＝1，2，……，N                          （7-4.3）

其中xij表示第i個變數xi的第j個測量數值。由上式得誤差的平方和為

                                                                            （7-4.4）

若以矩陣符號Y，A及X分別表示yi，ai及xij，

       

       

       

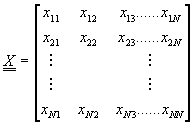
則誤差的平方和可寫成矩陣符號

                                                                             （7-4.5）

S達最小值的條件為，即

                                     （7-4.6）

故可得矩陣方程式

        X XT A＝X Y                                                                                    （7-4.7）

求解待定係數向量或近似模式之參數值得

                                                                           （7-4.8）

        將方程式（7-4.8）所得的係數AT＝[a1，a2，……，am]代回方程式（7-4.2），即得y對x1的線性迴歸方程式。

參考文獻

1. Whitaker, S., “Elementary Heat Transfer Analysis,” (1976).

2. Himmelblau, D.M., “Process Analysis by Statistical Methods” (1969).

3. Gerald, C.F., “Applied Numerocal Analysis” 3rd ed., Addison-Wesley, (1984)

4. 劉清田、王逢盛，”計算機套用程式—化學工程教學用程式”台北，(1982).

 

回首頁     回第二部     到第三部