第五章 非線性方程式
工程師所面對的真實世界，大部分都是非線性問題。本章所要討論的是非線性方程式或非線性聯立方程組的求解方法。非線性方程式可簡單寫成
，其中x = [x1，x2，……，xn]T ；f
= [f1，f2，……，fn]T。當n≠1時，即稱為聯立方程組。在工程及科學應用上，非線性聯立方程組的求解，是工程師時常會遇見的問題。例如設計問題D-V所表示的流體流速計算，微分方程式所得超越函數（Transcendental Equation）的求解，非理想氣體的P-v-T關係計算等等，均為常見的計算問題。
本章將依次探討多項式方程式、一般非線性方程式及非線性聯立方程組的求解方法。
第一節 葛瑞菲根平方法
在本章所介紹的各種求解方程式的方法中，葛瑞菲根平方法(Graeffe Root Square Method)是最能完整地求出一多項式所有根的方法，但其缺點是所求得的根只為近似解。因此，通常是利用葛瑞菲根平方法，先找出方程式所有根的大略位置，作為稍後所介紹的他種求根方法的敲門磚，再利用其他方法求出更正確的根。
假設ｎ次多項式ｆ(x) = 0之根
均為實數，且
。則多項式函數f (x)可寫成
（5-1.1）
（5-1.2）
或
（5-1.3）
定義輔助函數∮(x)為f(x)及f(-x)之乘積：
（5-1.4）
由於∮(x)為偶函數多項式，故可定義一新多項式f2(x)為
（5-1.5）
其根均為原多項式f (x) = 0之平方。重複此步驟，則我們可得到一序列多項式函數f2，f4，f8，……，
（5-1.6）
其中m為2的整數次方，而且fm
(x)之根為α1m，α2m，……，αnm。
又由於 |α1 |＞|α2 |＞……|αn |，因此，當m值足夠大以後，可以使得
（5-1.7）
將方程式（5-1.6）展開，整理後得到
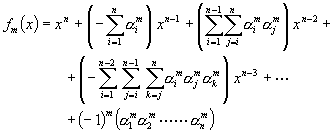（5-1.8）
將方程式（5-1.7）代入上式，簡化後可以得到
（5-1.9）
其中
因此，可得fm (x)之近似解為
（5-1.10）
由所得的第m組根，我們即可求得原方程式f (x) = 0之近似解。但由於這種方法在運作中將方程式的根作平方處理，因此，應特別注意，所得到的近似解的正負符號，仍需代入原方程式檢查才可確定。
第二節
假位法
假位法（False Position Method）又稱Regula Falsi，是一種最簡單的求解方程式根的方法，屬於較古老且低效率的一種方法。但是說明這種求解方程式的方法有助於了解求根的基本策略，因此，本節仍略加以說明。
假設已知方程式f (x) = 0，在a與b之間存在一個根r，其中a＜r＜b，則f (a) f (b)＜0。如圖5.2 (a)所示，連接（a，f (a)）及（b，f (b)）之直線必交x軸於（a，b）間之一點x1。由直線方程式得
(5-2.1)
此時，由於點1與（b，f (b)）同側，因此，以（x1，f (x1)）取代（b，f (b)）繼續利用方程式（5-2.1）求得下一近似值。
如圖5.2 (b)之情況，於第一次求解後以（x1，f (x1)）取代（b，f (b)），所得第二次近似根變成與（a，f (a)）同側，因此，改用（x2，f (x2)）取代（a，f (a)），再繼續進行求解過程。
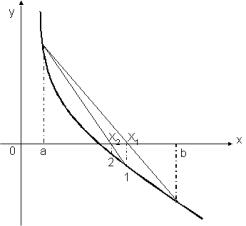
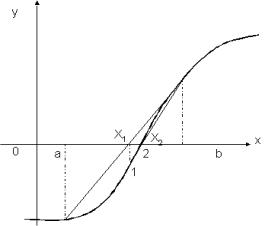
(a) 近似根位於根之同側 (b) 近似根位於根之異側
圖5.2 利用假位法求解方程式的根
第三節
割線法
割線法（Secant method）之迭代式與假位法相當類似，但其收斂速度較快。割線法是在根的附近利用直線來模擬原函數曲線。若方程式有實根，則直線將交x軸於該根附近，見圖5.3。x1及x2為迭代序列的兩個最初值，此二值可利用適當判斷方法選擇，或隨便猜測決定。
x1及x2點之函數值分別為f(x1)及f(x2)，則通過該二點之直線方程式為
（5-2.2）
直線與x軸之交點即為根之近似值，故假設該點之函數值f(x)=0，由上式得根之近似值為
（5-2.3）
所得的x值即圖5.3中的x3；再以（x2，f (x2)）及（x3，f (x3)）兩點作一新的直線，與x軸交點為x4。重複此程序，直到達到所要求的準確度或迭代至一定次數而未收斂時才停止。
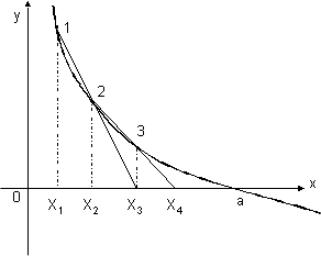
圖5.3 割線法求解方程式的根
割線法的一般式為：
（5-2.4）
割線法由於不必像假位法測試近似值之相對位置，因此，其執行速度較快；但其缺點則是必須有理想的最初猜測值，否則可能無法收斂。
第四節
韋格斯坦法
韋格斯坦法(Wegstein Method)採用投射迭代技巧。首先將方程式f(x) = 0改寫成x = g(x)的形式，再由g(x)曲線上的兩已知點投射求得第三點；然後連續利用最後所得的兩個x值，重複此投射步驟，求得新的嘗試值。如圖5.4，實線表函數值F =
g(x)，虛線表函數值F =
x，由於我們已將原方程式改寫成x = g(x)的形式，因此，點線與曲線的交點即表示方程式f(x) = 0之解。
由於韋格斯坦法係利用兩點投射，求得第三點，因此，可先利用直接代入法求得最初兩點，再進行投射。首先，由嘗試值x1開始，求得F1 = g(x1)；再利用虛線函數求得x2 = F1，建立最初的兩個據點（x1，F1）及（x2，F2）。1→2兩點所連成的直線方程式為：
1→2： 
（5-3.1）
與直線F = x之交點，可將F以x取代，代入上式，直接求得新的x值為
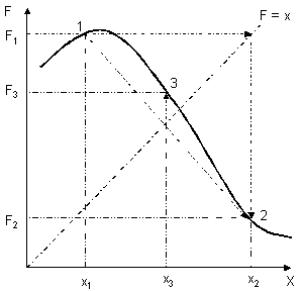
圖5.4 韋格斯坦法求解方程式的根
（5-3.2）
投射所得x3值，再利用F = g(x)，求得第3點之座標為（x3，F3）。然後再利用第2點及第3點重複此步驟，求出第四點座標。餘此類推，直到達到滿意的收斂程度為止。
韋格斯坦法收斂速度相當快，且在任何情況下均可收斂。而較簡單的直接迭代法及假位法[2，3]由於有不收斂及收斂速度慢的問題，因此，使用程度不如韋格斯坦法普遍。
第五節
牛頓法
設方程式f(x) = 0之準確根為a，x1表示a之近似解，則函數f(x)對x = x1之泰勒級數展開式為：
（5-4.1）
設x1與a之差為h，即a = x1 + h；代入上式可以得到
（5-4.2）
捨去h之二次方以上各項，且令二次方以上各項接近於0，則可以得到
（5-4.3）
解此方程式得到h的值為
（5-4.4）
由於方程式（5-4.2）中，h的二次方以上各項都被我們捨去，因此，x1 + h值可能不等於準確根a，但其值能夠較x1更為接近準確的根a，仿照這種方法，可類推得到迭代近似值的表示式為
（5-4.5）
利用方程式（5-4.5）求得方程式f(x)之近似根的方法稱為牛頓法(Newton’s Method)。由方程式（5-4.2）知牛頓法的捨去誤差為h2項，表示第n個近似根的誤差為0.1時，第n + 1個近似根的誤差約為(0.1)2 = 0.01，因此，收斂速度相當快。但使用牛頓法解方程式時，應該注意這種方法有兩個缺點：(一)起始值若不在根之附近，利用牛頓法時常無法收斂。因此，實際應用時，最好能配合他種數值方法先找出根之大略位置，再利用牛頓法求得根之近似解。(二)利用牛頓法進行計算時，必須使用一次導函數f’(x)，對於較複雜的方程式，使用者必須小心縯導求出f’(x)。此外，若在根的附近f’(x)很小時，f(x)的計算誤差會在求f(x) / f’(x)時被放大，使得所得到的根準確度變差。
就計算效率的觀點而言，割線法每一次迭代只需計算一個函數值，而牛頓法則需計算f(x)及f’(x)兩個函數值，計算效率略差，因此，一般性的計算機程式大部分採用割線法來設計。
第六節
非線性聯立方程式
本書第四章中曾探討了線性聯立方程式的求解方法，比較起來非線性聯立方程式的求解就可能略為困難，其原因有二：(1)非線性聯立方程式通常無法求得真正的解；(2)非線性聯立方程式可能有一組以上的解。因此，通常需利用電子計算機以迭代法來尋求方程組的解﹔但迭代法只能找出一組可能的解﹔而無法一次找出所有可能的解。因此，要找出一組非線性聯立方程式的所有可能解，就必須由不同的起始值開始進行迭代，這項缺點相當不易克服。所幸在大部分工程或科學系統中，通常只有一組解具有實際的物理意義，其他的解可能都存在於無意義的範圍（例如壓力或濃度為負值）。
解非線性聯立方成組的方法，常見的方法有三種：
1. 連續取代法（Successive substitution）
2. 牛頓拉福森法（Newton-Raphson method）
3. 函數極小化法（Function minimization）
第七節中，我們將介紹連續取代法；第八節中介紹牛頓拉福森法﹔第九節中介紹利用數值方法求斜率，以改良牛頓拉福森法所得的割線法。函數極小化法由於牽涉較複雜的數學處理，因此，不列入本書討論範圍，有興趣讀者請參考文獻[5，6]。
第七節 連續取代法
連續取代法解單一方程式或聯立方程組基本原理完全相同，唯一的差別是後者每一次迭代需重新估計一個以上的變數。假設我們要解以下的聯立方程組：
（5-6.1）
（5-6.2）
（5-6.3）
（5-6.4）
（5-6.5）
首先，可先將原方程組
改寫成x = g(x)的型式，如
（5-6.6）
（5-6.7）
（5-6.8）
（5-6.9）
（5-6.10）
我們若提供一組最初假設值，代入方程式（5-6.6）至（5-6.10），即可求得一組新的近似值，重複此步驟直到收斂為止。利用上述策略有時可能不穩定，且會發散至無窮大而無法收斂至一組定值。雖然，利用其導函數可判斷系統是否會穩定，但由於求導函數過程相當繁瑣，少有人真正願意去測試，較常見的做法倒是試著解解看，如果不收斂，再更換一組
的轉換方式，直到能求得收斂的結果為止。
利用導函數判斷系統
迭代方式為收斂的準則為
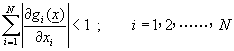（5-6.11）
第八節
牛頓拉福森法
牛頓拉福森法和解單一方程式所使用的牛頓法相當類似，例如考慮兩個聯立方程式：
（5-7.1）
（5-7.2）
首先估計一組近似解x1,0，x2,0，若這組近似解與正確解之距離為h1及h2，則將函數f1及f2作泰勒級數展開，並捨去h2以上諸項，得到
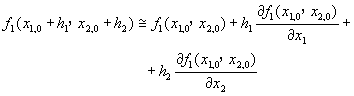（5-7.3）
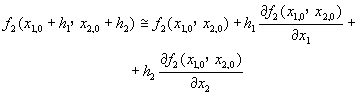（5-7.4）
我們的目的是希望讓x1,0+ h1及x2,0+ h2變成方程組的解，因此，要求f1(x1,0+ h1，x2,0 + h2) = 0，且f2(x1,0 + h1，x2,0 + h2) = 0。故方程式（5-7.3）及（5-7.4）右側均等於零。而方程式中f1(x1,0，x2,0)及f2(x1,0，x2,0)分別代表方程式（5-7.1）及（5-7.2）的殘餘值，只要將近似解(x1,0，x2,0)代入，即可計算求出。四個導函數分別為各方程式殘值的x1,0及x2,0導函數，只要能求得其導函數表示式，再將近似解x1,0及x2,0代入式中，即可求得各導函數值。故方程式（5-7.3）及（5-7.4）可改寫成：
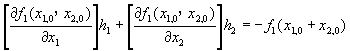（5-7.5）
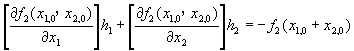（5-7.6）
此方程組含有兩個線性方程式及兩個未知數h1及h2，故可解出h1及h2，求得較佳的近似解x1,0 + h1及x2,0 + h2。這種方法可認為是將一組非線性聯立方程式簡化成一組線性聯立方程式，只要利用第四章所介紹的方法即可求得其解。但由於我們以將原非線性方程組作線性化近似處理，因此，所得的解並非正確解，必須重複迭代，以求得準確的解。
仿上述方法，若考慮含n個方程式的聯立方程組
（5-7.7）
則我們首先定義導函數矩陣
稱為
（5-7.8）
其中
（5-7.9）
導函數矩陣
稱為Jacobian，其中
。再定義向量
為：
（5-7.10）
最初估計的近似解向量為
。
之迭代式為：
（5-7.11）
其中
則仿方程式（5-7.5）及（5-7.6）為下列線性聯立方程組之解：
（5-7.12）
利用牛頓拉福森法最重要的要求是所有導函數的數值都必須能夠求得。牛頓拉福森法每一次迭代都需要重新計算這些導函數值。這種方法收斂速度雖然相當快，但需不斷的計算大量的導函數是其最大的缺點。此外，程式設計雖簡單，但要在紙上作業先導出n2個導函數卻是一件即令人無法忍受的工作，想想看，如果要解20個非線性聯立方程式，就得先導出400個導函數呢！
第九節
牛頓拉福森割線法
牛頓拉福森法收斂速度相當快，但最大的缺點是使用者必須先縯導利用此方法所必備的n2個偏微分表示式，以建立Jacobian矩陣。當方程式數目n很大時，這項工作將變得相當沉重。本書第六章將討論數值微分及積分，利用數值微分的技巧，就可以將微分工作交由計算機處理。牛頓拉福森割線法正是利用這種方法克服此困難，割線法的基本原理與牛頓拉福森法完全相同，唯一的差別是導函數不必先行縯導，而是直接利用原方程式作數值微分求得。
由於在工程科學上的應用，通常方程式的數目都相當多，而且函數可能相當複雜，不易求得偏微分表示式，因此，利用割線法將遠較牛頓拉福森法便捷。而就程式執行速度及收斂性質而論，二者則完全相同，因此，本書推薦讀者宜盡量使用割線法，而不採用牛頓拉福森法。
第十節
牛頓拉福森割線法與Excel應用
牛頓拉福森割線法的基本原理與牛頓拉福森法完全相同，唯一的差別是導函數直接利用原方程式作數值微分求得。這種特性尤其適合利用Excel編寫程式。以下利用實例說明如何使用及編寫Excel版的牛頓拉福森割線法程式。
例5-9 牛頓拉福森割線法與Excel
編寫Excel版的牛頓拉福森割線法程式，重解例5-6。
解: 利用Excel編寫之程式如下所示﹔
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
1 |
F1= |
|
Jacobian |
|||||||
|
2 |
|
|||||||||
|
3 |
F2= |
|
||||||||
|
4 |
||||||||||
|
5 |
F3= |
|
X increment |
Ex= |
1.000E-03 |
|
|
|||
|
6 |
|
|
|
|
|
|||||
|
7 |
|
Initial Trial |
x + dx |
x - dx |
|
-F(x) |
|
|
|
|
|
8 |
U1 |
1.000E+00 |
1.001E+00 |
1.000E+00 |
|
7.800E-01 |
|
|
|
|
|
9 |
U2 |
1.000E+00 |
1.001E+00 |
1.000E+00 |
|
-5.890E+01 |
|
|
|
|
|
10 |
U3 |
1.000E+00 |
1.001E+00 |
1.000E+00 |
|
1.040E+02 |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
12 |
x+dx |
U1 |
U2 |
U3 |
x-dx |
U1 |
U2 |
U3 |
|
|
|
13 |
F1 |
-7.790E-01 |
-7.790E-01 |
-7.828E-01 |
|
-7.800E-01 |
-7.800E-01 |
-7.800E-01 |
|
|
|
14 |
F2 |
5.898E+01 |
5.882E+01 |
5.890E+01 |
|
5.890E+01 |
5.890E+01 |
5.890E+01 |
|
|
|
15 |
F3 |
-1.040E+02 |
-1.039E+02 |
-1.040E+02 |
|
-1.040E+02 |
-1.040E+02 |
-1.040E+02 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
17 |
Jacobian |
Inverse Jacobian |
|
h |
||||||
|
18 |
|
1.000E+00 |
1.000E+00 |
-2.780E+00 |
|
8.876E-02 |
1.138E-02 |
1.028E-02 |
|
4.674E-01 |
|
19 |
|
8.004E+01 |
-8.004E+01 |
0.000E+00 |
|
8.876E-02 |
-1.109E-03 |
1.028E-02 |
|
1.203E+00 |
|
20 |
|
0.000E+00 |
8.004E+01 |
2.401E+01 |
|
-2.959E-01 |
3.696E-03 |
7.393E-03 |
|
3.204E-01 |
|
21 |
|
|
|
|
|
|
|
|
|
|
|
22 |
#1 |
Trial Value |
x + dx |
x - dx |
|
-F(x) |
|
|
|
|
|
23 |
U1 |
1.467E+00 |
1.469E+00 |
1.467E+00 |
|
3.153E-14 |
|
|
|
|
|
24 |
U2 |
2.203E+00 |
2.205E+00 |
2.203E+00 |
|
4.915E+01 |
|
|
|
|
|
25 |
U3 |
1.320E+00 |
1.322E+00 |
1.320E+00 |
|
-5.909E+01 |
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
27 |
x+dx |
U1 |
U2 |
U3 |
x-dx |
U1 |
U2 |
U3 |
|
|
|
28 |
F1 |
1.467E-03 |
2.203E-03 |
-3.671E-03 |
|
-1.467E-06 |
-2.203E-06 |
3.671E-06 |
|
|
|
29 |
F2 |
-4.897E+01 |
-4.953E+01 |
-4.915E+01 |
|
-4.915E+01 |
-4.914E+01 |
-4.915E+01 |
|
|
|
30 |
F3 |
5.909E+01 |
5.948E+01 |
5.913E+01 |
|
5.909E+01 |
5.909E+01 |
5.909E+01 |
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
32 |
Jacobian |
Inverse Jacobian |
|
h |
||||||
|
33 |
|
1.000E+00 |
1.000E+00 |
-2.780E+00 |
|
8.358E-02 |
7.803E-03 |
7.329E-03 |
|
-4.960E-02 |
|
34 |
|
1.174E+02 |
-1.763E+02 |
0.000E+00 |
|
5.567E-02 |
-4.740E-04 |
4.881E-03 |
|
-3.117E-01 |
|
35 |
|
0.000E+00 |
1.763E+02 |
3.170E+01 |
|
-3.096E-01 |
2.636E-03 |
4.392E-03 |
|
-1.300E-01 |
|
36 |
|
|
|
|
|
|
|
|
|
|
|
37 |
#2 |
Trial Value |
x + dx |
x - dx |
|
-F(x) |
|
|
|
|
|
38 |
U1 |
1.418E+00 |
1.419E+00 |
1.418E+00 |
|
3.508E-14 |
|
|
|
|
|
39 |
U2 |
1.892E+00 |
1.893E+00 |
1.892E+00 |
|
3.813E+00 |
|
|
|
|
|
40 |
U3 |
1.190E+00 |
1.192E+00 |
1.190E+00 |
|
-4.119E+00 |
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
42 |
x+dx |
U1 |
U2 |
U3 |
x-dx |
U1 |
U2 |
U3 |
|
|
|
43 |
F1 |
1.418E-03 |
1.892E-03 |
-3.309E-03 |
|
-1.418E-06 |
-1.892E-06 |
3.309E-06 |
|
|
|
44 |
F2 |
-3.652E+00 |
-4.099E+00 |
-3.813E+00 |
|
-3.813E+00 |
-3.813E+00 |
-3.813E+00 |
|
|
|
45 |
F3 |
4.119E+00 |
4.405E+00 |
4.153E+00 |
|
4.119E+00 |
4.119E+00 |
4.119E+00 |
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
47 |
Jacobian |
Inverse Jacobian |
|
h |
||||||
|
48 |
|
1.000E+00 |
1.000E+00 |
-2.780E+00 |
|
7.821E-02 |
8.123E-03 |
7.607E-03 |
|
-3.586E-04 |
|
49 |
|
1.135E+02 |
-1.514E+02 |
0.000E+00 |
|
5.862E-02 |
-5.166E-04 |
5.701E-03 |
|
-2.545E-02 |
|
50 |
|
0.000E+00 |
1.514E+02 |
2.858E+01 |
|
-3.105E-01 |
2.736E-03 |
4.787E-03 |
|
-9.285E-03 |
|
51 |
|
|
|
|
|
|
|
|
|
|
|
52 |
#3 |
Trial Value |
x + dx |
x - dx |
|
-F(x) |
|
|
|
|
|
53 |
U1 |
1.417E+00 |
1.419E+00 |
1.417E+00 |
|
2.665E-15 |
|
|
|
|
|
54 |
U2 |
1.866E+00 |
1.868E+00 |
1.866E+00 |
|
2.781E-02 |
|
|
|
|
|
55 |
U3 |
1.181E+00 |
1.182E+00 |
1.181E+00 |
|
-2.901E-02 |
|
|
|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
|
57 |
x+dx |
U1 |
U2 |
U3 |
x-dx |
U1 |
U2 |
U3 |
|
|
|
58 |
F1 |
1.417E-03 |
1.866E-03 |
-3.283E-03 |
|
-1.417E-06 |
-1.866E-06 |
3.283E-06 |
|
|
|
59 |
F2 |
1.330E-01 |
-3.065E-01 |
-2.781E-02 |
|
-2.797E-02 |
-2.753E-02 |
-2.781E-02 |
|
|
|
60 |
F3 |
2.901E-02 |
3.077E-01 |
6.250E-02 |
|
2.901E-02 |
2.873E-02 |
2.897E-02 |
|
|
|
61 |
|
|
|
|
|
|
|
|
|
|
|
62 |
Jacobian |
Inverse Jacobian |
|
h |
||||||
|
63 |
|
1.000E+00 |
1.000E+00 |
-2.780E+00 |
|
7.764E-02 |
8.130E-03 |
7.610E-03 |
|
5.382E-06 |
|
64 |
|
1.134E+02 |
-1.494E+02 |
0.000E+00 |
|
5.897E-02 |
-5.198E-04 |
5.781E-03 |
|
-1.821E-04 |
|
65 |
|
0.000E+00 |
1.494E+02 |
2.836E+01 |
|
-3.106E-01 |
2.738E-03 |
4.817E-03 |
|
-6.358E-05 |
1. 首先定義U1, U2, U3的初步猜測值，並計算-F(x)放置在F8..F10位置。
2.
依牛頓拉福森割線法需計算導函數矩陣Jacobian，編寫程式時，將
及
計算放置在C8..C10及D8..D10位置，將
及
計算放置在B13..D15及F13..H15位置。
3.
計算導函數矩陣Jacobian﹔
，放置在B18..D20位置。
4. 計算反矩陣，先選取F18..H20區域，輸入=Minverse(B18..D20)，再輸入<Ctrl><Shift><Enter>，即可得到反矩陣值。Minverse(Array)為Excel內建的反矩陣運算函數。
5. 計算h陣列，先選取J18..J20區域，輸入=Mmult(F18..H20,F8..F10)，再輸入<Ctrl><Shift><Enter>，即可得到h值。Mmult(Array 1, Array 2)為Excel內建的陣列乘法運算函數。
6. 計算所得x新的嘗試值為x + h。選取第7至21列區域，作複製，成第22至36列。修改U1的新嘗試值B23為=B8+J18。複製B23到B24及B25。即得到第一次計算結果。
7.
選取第22至36列區域，作複製，成第37至51列。即得到第二次計算結果。餘此類推。
由計算結果可以發現到第三次計算，計算誤差增量h即小到10-4以下，顯示收斂效果相當良好。計算結果與例5-6一致。
Excel程式編寫容易，但一般而言，若聯立方程式的數目較多時，由於導函數矩陣需一一輸入，較容易造成人為疏忽，應特別注意。讀者可參考本例題做法，嘗試其他數值方法的程式編寫。
參考文獻
1. Coulson, J. M., J. F. Richardson, “Chemical Engineering”,
Vol.2, 3rd Ed., Pergamon Press, (1982).
2. Carnahan, B., H. A. Luther, and J. O. Wilkes, “Applied
Numerical Methods” Wiley, (1970).
3. Traub, J. F., “Iterative Methods for the Solution of
Equations”, Prentice-Hall, (0964).
4. Henley, E. J., and E. M. Rosen, “Material and Energy Balance
Computation”, Wiley, (1969).
5. Box, M. J., Davies, D. and Swann, W. H., “Nonlinear
Optimization Techniques”, ICI Monograph No.5, Oliver & Boyd, London,
(1969).
6. Murray, W. (Ed) “Numerical Methods for Unconstrained Optimization”, Academic Press, London, (1972).
