回首頁     回第二部     下一章

第四章 聯立線性方程式

        設計問題D-IV中，總共有9個流體流束，每一流束中都含有A、B及C三種化合物。除了流束中A、B及C的流量為已知以外，我們總共有24個未知數需要求解，因此，可預測總共需要建立24個獨立的方程式。這只是一個相當簡化的工程問題，就需建立如此多的方程式，可推想一個實際化學工廠或其他生產工廠的質量平衡計算將是如何繁重的工作。因此，借助於有效率的計算機程式解決大量的質量及能量平衡計算，乃成為工程師經常需要面對的問題。

第一節           聯立線性方程式

化工程序的質量平衡計算，常需求解大量的聯立代數方程式。以設計問題D-IV為例，我們可就各操作單元分別建立方程式：

單元1：混合加熱器.    用於將混合物加熱至反應器所要求的入口溫度。在此單元中進料與回流混合及加熱後，變成流束，故各成分之質量平衡方程式為

                                                                            (4-1.1)

                                                                            (4-1.2)

                                                                            (4-1.3)

單元2：反應器.    在反應器中，進行反應A→C及B→C，其中A的轉變率為0.30，B的轉化率為0.50，反應器之進料為及，因此，

                                                              (4-1.4)

                                                              (4-1.5)

                            (4-1.6)

單元3：閃蒸塔.    提供熱量，使進入本單元的部分混合物蒸發，由於化合物C之沸點較A及B低，故蒸氣中C的含量即增高。根據已知條件

                                                                                   (4-1.7)

                                                                                    (4-1.8)

                                                                                    (4-1.9)

               又由於，所以可以得到下列平衡式

                                                                            (4-1.10)

                                                                            (4-1.11)

                                                                            (4-1.12)

單元4：冷卻分離器.    將進料冷卻，使液相含有較高濃度的A及B，並部分回流至單元2。由已知條件：

                                                                            (4-1.13)

                                                                              (4-1.14)

                                                                             (4-1.15)

               又由於，因此，可以得到

                                                                          (4-1.16)

                                                                                         (4-1.17)

                                                                         (4-1.18)

單元5：蒸餾塔.    用於提高產品中所含C的濃度，根據已知數據：

                                                                              (4-1.19)

                                                                              (4-1.20)

                                                                                 (4-1.21)

               又因為，所以可將各成分之平衡式寫成

                                                                 (4-1.22)

                                                                 (4-1.23)

                                                                (4-1.24)

        我們總共得到24個變數及24個方程式。在建立以上方程組的時候，我們假設此系統已經是經過長時間的操作，並且已經達到“穩定狀態”(Steady State)，因此，各成分之流量不會隨時間而變。

        在以上24個方程式中，我們可發覺每一項中只含一個未知數，這類方程式我們即稱為線性聯立方程式。 若將以上24組方程式寫成矩陣形式，則可以得到

                                                                                             (4-1.25)

其中為係數矩陣，，為常數向量。

        在本章中，我們將以實際問題為例，說明聯立線性方程式的各種求解方法。我們將依次介紹最常使用的三種線性聯立方程式解法，『高斯消去法（Gauss Elimination）』、『高斯佐丹消去法（Gauss-Jordan Elimination）』，及『高斯賽德迭代法（Gauss – Seidel Iterative Method）』，最後，再介紹三對角線矩陣方程式(Tri-diagonal Equations)的解法。

第二節           高斯消去法

由於任何方程式乘上常數均不會改變其解答，而且，任何方程式均可利用兩方程式的和或差來取代，因此，我們可利用這種方法找出方程式的解；而這種方程組的求解方法，若利用矩陣的乘法及加法來進行，就稱為高斯消去法。

高斯消去法的基本運算原則，是利用任何方程式乘上常數都不會改變其解答的原理，將原方程組乘以適當的常數後，作相互加減處理，使係數矩陣的對角線全部變成1，且使其左下角元素全變成0，再由最後一個方程式由下往上代入，即可求出方程組的解。

基本上高斯消去法是一種相當規則化的求解線性聯立方程式的方法。由於具有規則性，因此，非常適合寫成計算機程式。但由於計算過程略為繁複，因此，比較不適合用於手算求解。此外，由於演算過程中需作大量的四則運算（＋，－，×，÷），因此，方程式數量龐大時，其準確性相對堪虞。高斯消去法的計算時間約與方程數目的三次方成比例，即解6個方程式所需時間約為3個方程式的8倍。

以下用簡單的方程組說明高斯消去法的基本運算方式。首先考慮以下的線性聯立方程組：

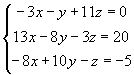                                                                                (4-2.1)

若將聯立方程組寫成矩陣形式，則係數矩陣及常數向量分別為

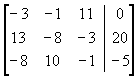                                                                              (4-2.2)

將第一列除以-3後寫回第一列，第二列除以13再減去第一列，第三列除以-8再減去第一列，則可以得到

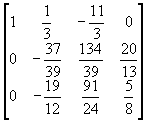                                                                           (4-2.3)

        上式中，第二及第三列的第一個元素均已變成0。重複這種步驟，將第二列乘以，使對角線元素變成1。第三列乘以再減去所得的第二列結果，就可以得到新的矩陣方程式如下所示：

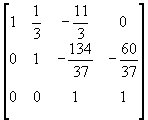                                                                           (4-2.4)

亦即經過高斯消去處理以後，對應的三方程式為

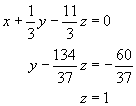                                                                              (4-2.5)

由第三方程式得z = 1，代回第二方程式得y = 2，再代回第一方程式，得x = 3。以上的運算過程即稱為高斯消去法。

        對計算機運算而言，我們必須設法使捨入誤差減小，以提高運算之準確度。在高斯消去法中，我們可將每一行的最大元素作為運算轉軸，例如將方程式改寫成

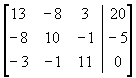
        即第一次消去後，得到

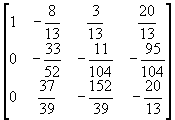
        由於，故第二次消去前先將第二列及第三列交換，再進行消去操作。利用這種方式可提高準確度（詳見[1]），此外，亦可防止以“0”作為轉軸而產生執行錯誤。

第三節           高斯佐丹法

高斯佐丹法基本上與高斯消去法相當類似，但是高斯佐丹法也較高斯消去法略為複雜，高斯消去法是將主對角線以下的元素消去成為零，而將主對角線上各元素變成1。高斯佐丹法求解時，則是將對角線以外的元素仿照高斯消去法的原理完全消去，剩下對角線元素，並將對角線元素完全變成1。因此，高斯佐丹法除了能解出方程式的解以外，同時更進一步可以求得常數矩陣的反矩陣，因此，使用價值相對較高。

但由於高斯佐丹法和高斯消去法運算方式相似，因此，與高斯消去法具有相同的優點及缺點。執行時間約與矩陣階次n的三次方成正比，且由於運用大量的乘、除及加法運算，因此，準確度較差。

假設一線性聯立方程式以矩陣符號表示為

                                                                                                  (4-3.1)

將矩陣利用消去法將非對角線元素完全消去，且使主對角線元素變成1，即等於將變成（單位矩陣）。由於

                                                                                                 (4-3.2)

故將方程式（4-3.1）兩邊各乘以反矩陣，得到

                                                                                                   (4-3.3)

        在化學工程程序質能平衡計算時，我們常需假設數種進料組成或流量，分別求解以後，以求得最適設計條件。如設計問題D-IV，進料的組成或流量改變時，方程式（4-1.1）至（4-1.24）的係數矩陣並不受影響，只有常數矩陣改變。由於利用高斯佐丹法求解（4-3.1）時，可以同時求得，因此，常數矩陣中若同時存放m組不同的數據，則在高斯佐丹消去後，利用與的乘積，即可同時求得m組不同條件下的解答。

        程式規劃時，可將反矩陣與矩陣放在同一存放位置，所得到的方程式解及常數矩陣亦可放在同一位置，亦即呼叫高斯佐丹法副程式前放置係數矩陣及常數矩陣的及，在執行高斯佐丹消去法後，則存放及。

第四節           高斯賽德迭代法

前面兩節所述高斯消去法及高斯佐丹消去法由於使用大量的乘、除及加法運算，因此，矩陣方程式較大時，運算所產生的誤差將變的愈為明顯，而使這兩種方法所得結果變成無意義。遇到這種情況，可考慮使用高斯賽德迭代法（Gauss-Seidel Iterative method）。高斯賽德迭代法是利用依序迭代求解聯立線性方程組的方法。其基本做法是給定一最初近似值，然後利用方程式進行重複迭代，直到結果接近真正解答為止。由於這種方法每一次近似計算只跟前一近似值有關，因此，捨入誤差（Round-off error）不會因連續運算而累積。此外，由於採用迭代趨近法，因此，方程式非線性時亦可採用同一策略進行求解。

考慮方程式（4-2.1）所示之聯立線性方程組

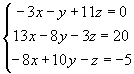                                                                                (4-2.1)

我們可利用第一式求得x的迭代表示式：

                                                                                              (4-4.1)

式中x為前一迭代所得y及z值的函數，例如，最初近似值設x，y，z均為0，則第一次迭代所得x值亦為0。同理利用第二式求得y的迭代近似表示式為：

                                                                                        (4-4.2)

此時，x值仍為0，z值亦為0，代入方程式中得到y = -2.5。利用第三式求解z，得

                                                                                             (4-4.3)

此時，x值為0，y值的第一次迭代值為-2.5，故得到z的第一次迭代值為z = -20，利用此一策略所得迭代結果如下：

迭代次數

0

0.00

0.00

0.00

1

0.00

-2.50

-20.00

2

-72.50

-112.81

-543.13

3

-1,953.85

-2,973.84

-14,102.58

4

-50,718.17

-77,131.06

-365,560.26

5

-1,314,677.25

-1,999,267.94

-9,475,256.39

6

-34,076,184.11

-51,820,580.54

-245,596,327.47

7

-883,246,340.53

-1,343,176,683.06

-6,365,796,101.38

        很顯然地，迭代結果並不收斂而且快速發散。可以推想，應該是處理策略上不正確所導致。觀察方程式(4-4.1)，若z與真實的解有誤差，則由方程式可知，x的誤差將與z的誤差擴增11倍。同理，由方程式(4-4.2)可知y的誤差將比x的誤差擴大13倍。z的誤差將比y的誤差擴大10倍。因此，或因迭代計算使得誤差快速成長。

根據這種觀察，我們若能將方程式的最大係數作為除數，則應該能使誤差逐漸減小。以下我們以同一組方程式為例，實際了解策略上的改變對迭代收斂性的影響。首先將方程式（4-2.1）的次序調動，使最大元素均在主對角線上：

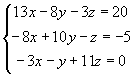                                                                              (4-4.4)

仿照前面的做法，則對應的迭代方程式可變成

                                                                                             (4-4.5)

                                                                                                 (4-4.6)

                                                                                                      (4-4.7)

觀察這些方程式，由於除數均為該方程式中之最大數，其他變數的誤差值經演算後應該都會被乘以一個比1小的數字，使得誤差逐漸縮小。

利用方程式(4-4.5)、(4-4.6)及(4-4.7)，仍由x，y，z均為0開始迭代，所得迭代結果為：

迭代次數




0

0.000000

0.000000

0.000000

1

1.538462

0.730769

0.486014

2

2.100323

1.228860

0.684530

3

2.452651

1.530574

0.808048

4

2.666826

1.714265

0.883158

5

2.797200

1.826076

0.928880

21

2.999928

1.999938

0.999975

22

2.999956

1.999962

0.999985

23

2.999973

1.999977

0.999991

由以上結果可發現迭代值快速趨近（3，2，1）。上述兩種迭代所得結果完全不同，唯一的差別是後者將係數矩陣的最大元素均排列在主對角線上。因此，利用高斯賽德迭代法設計程式時，必須將係數矩陣的最大元素均排列在主對角線上。

此外，設計程式時，亦可引入緩衝係數（λ），使迭代的收斂速率增快。例如，上述迭代法第J次所得X值為X（J），次一迭代所得為，則利用緩衝法，所得新的X（J + 1）值為

                                                                   (4-4.8)

當λ = 1時，即與前述未作緩衝處理的方法相同。一般而言，緩衝係數λ值範圍介於0至2間，亦即0<λ<2。

第五節           聯立線性方程式之解法比較

高斯消去法及高斯佐丹消去法需涉及大量的乘除及加法運算，因此，當係數矩陣階數較高時，其捨入誤差可能變得相當可觀。高斯賽德迭代法由於利用重複迭代逼近正確解，因此，沒有捨入誤差累積的問題，但有時無法收斂且矩陣階數低時，迭代法通常較為耗時。比較三種方法的算數運算次數分別為：

高斯消去法

（全部過程）

高斯佐丹法

（全部過程）

高斯賽德法

（每次迭代）

因此，以n = 100為例，利用高斯消去法約需作68,1550次算數運算，利用高斯賽德迭代法每次迭代約需運算19,900次，因此，若迭代次數超過34次（約為n / 3），則後者可能略為費時。但後者縱使略為費時，由於其捨入誤差小，故仍甚具價值。

第六節           三對角線矩陣方程式 

三對角線矩陣方程式（Tridiagonal matrix equation）或亞可比矩陣（Jacobi matrix）方程式，在各種工程及化工應用上極為常見，例如蒸餾、吸收、反應器（CSTR）設計等，或利用有限差分法解邊界值問題時均可能出現。

三對角線矩陣方程式由於其係數矩陣除了三個對角線外，其他元素均為零，因此，利用高斯消去法求解並不划算。如果將三對角線矩陣方程式視為一般矩陣方程式進行求解，則需使用N2個記憶位置，且其運算也需耗費很長的時間。以下介紹一種效率較高的處理方式。

典型的三對角線矩陣方程式，如：

                                                                                                 (4-6.1)

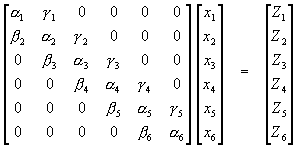                                     (4-6.2)

係數矩陣中非零元素只有（3 N - 2）= 16個，如果我們能妥善地利用此性質，則可使求解過程顯著簡化，並提高執行效率。

        將係數矩陣上下分解（Lower-Upper decomposition）成兩個雙對角線矩陣（Bi-diagonal form）之乘積：

                                                                                     (4-6.3)

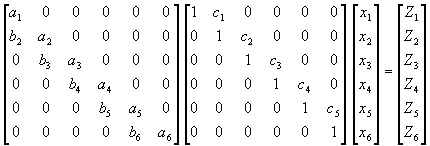    (4-6.4)

由於，因此，比較對應的各項，可以得到：

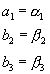
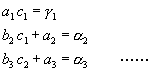
或寫成

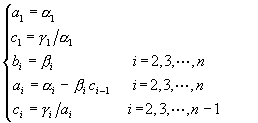                                                  (4-6.5)

由於，令，則可將原方程式寫成：

                                                                                                    (4-6.6)

或

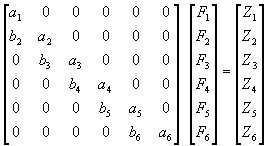                                               (4-6.7)

由上往下代入，解此方程式，得

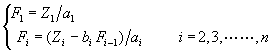                                             (4-6.8)

求得向量以後，在利用求解向量，由於

                                                     (4-6.9)

由最下方往上代入（與高斯消去法很相似的做法），即可解出X為：

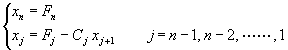                                      (4-6.10)

第七節           利用Excel解聯立方程式

本章所介紹的各種線性聯立方程式解法，雖然簡單易用，但程式編寫仍有一定的複雜度。近年來，由於Microsoft Excel的普遍使用，工程人員亦可善用Microsoft Excel內建的反矩陣運算函數Minverse(Array)及矩陣乘法運算函數Mmult(Array 1, Array 2)，做為求解線性聯立方程式或求反矩陣的工具。回顧本章第三節，我們可將線性聯立方程式以矩陣符號表示為

                                                                                                  (4-7.1)

其解答為

                                                                                               (4-7.2)

亦即，要求解聯立方程式(4-7.2)，只要先求出反矩陣，再利用矩陣乘法，即可求出解答。在Excel中，有兩個簡單易用的矩陣操作函數，(1)反矩陣運算函數Minverse(Array)，及(2)矩陣乘法運算函數Mmult(Array 1, Array 2)﹔正好可以作這兩種運算。

以方程式(4-7.2)為例，定義矩陣A以後，利用Minverse(A)即可得到反矩陣值A-1﹔然後，定義陣列B，再利用Mmult(A-1,B)即可得到解答X。

例4.5  利用Excel解聯立方程式

利用Excel解下列聯立方程式

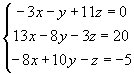
解:  利用Excel解上列聯立方程式，如下表所示:

 

A

B

C

D

E

F

G

H

1

矩陣A

 

 

 

矩陣B

 

 

 

2

 

-3

-1

11

 

0

 

 

3

 

13

-8

-3

 

20

 

 

4

 

-8

10

-1

 

-5

 

 

5

 

 

 

 

 

 

 

 

6

反矩陣A-1

解答 X = A-1B

 

7

 

0.06609

0.18957

0.15826

 

3

 

 

8

 

0.06435

0.15826

0.23304

 

2

 

 

9

 

0.11478

0.06609

0.06435

 

1

 

 

 

程式編寫方法：

1.      首先在B2..D4輸入係數矩陣A

2.      在F2..F4輸入常數陣列B

3.      圈選B7..D9，輸入=Minverse(B2..D4)

4.      然後同時按<Ctrl> <Shift> <Enter>，則B7..D9將出現矩陣A的反矩陣值

5.      圈選F7..F9，輸入=Mmult(B7..D9,F2..F4)

6.      然後同時按<Ctrl><Shift> <Enter>，則F7..F9將出現答案陣列X值

注意: 在Excel應用上，需使用<Ctrl><Shift><Enter>代表函數輸入。

第八節           矩陣特徵值

對於一個方矩陣A，若存在一個非為零的陣列u，使得該矩陣A與陣列u的乘積等於陣列u與一特定常數的乘績，則稱該特定常數為矩陣的特徵值(Eigenvalue)，u即稱為矩陣的特徵陣列(Eigenvector)。

以數學符號表示，可以寫成

                                                                                                 (4-8.1)

或

                                      (4-8.2)

利用方程式(4-8.2)可以建立矩陣的特徵方程式為。

例4.6  矩陣之特徵值

試求矩陣A之特徵值。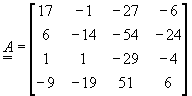 

[解]

        利用方程式(4-8.2)展開，得到矩陣A的特徵方程式為

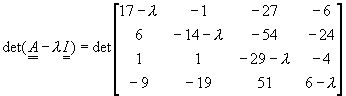
解此特徵方程式，得到矩陣的特徵值為-30，-20，10及20。

魯逖髾瑟L-U分解法

        方矩陣的特徵值在解微分方程式問題的應用上，常需使用，是一種很重要的數學技巧。但是利用以上所介紹的方法解方矩陣的特徵值，當矩陣元素較多時，將變得即為複雜，而不切實際。魯逖髾瑟(Rutishauser，[6])提出的L-U分解法，是求解方矩陣特徵值得一個有效率的方法。

首先假設方矩陣A=A1，同時假設可以將方矩陣A改寫成上三角形矩陣R及下三角形矩陣L的乘績

                                                       (4-8.3)

其中Lk為對角線元素均為1，且在對角線以上的元素均為零的下三角形方陣，Rk為對角線以下的元素均為零的上三角形方陣。

由於，可以得到，及。而又由於，若將L1及R1的表示式分別代入中，可以得到

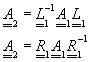
連續重複執行此步驟，可以得到的表示式為

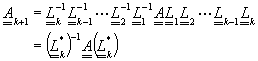                                               (4-8.4)

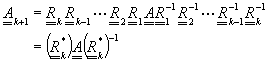                                             (4-8.5)

與方矩陣A相似，且有相同的特徵值及特徵陣列。假設為有限下三角形方陣，當k值趨近於無窮大時，會趨近於定值。亦即

                                                                 (4-8.6)

k值增加1時，仍會相同，亦即。代回方程式(4-8.3)，得到

                                                                              (4-8.7)

將方程式(4-8.7)代入方程式(4-8.4)，得到

                                                                                      (4-8.8)

其中R與A有相同的特徵值，而且若A的特徵值為實數，則其特徵值即為R的對角線元素。

又由於由方程式(4-8.3)知道，因此

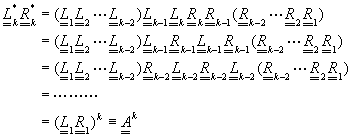                                (4-8.9)

令，B=(bij)﹔C為對角線元素均為1，且在對角線以上的元素均為零的下三角形方陣，C=(cij)﹔D為對角線以下的元素均為零的上三角形方陣，D=(dij)。則利用矩陣運算方式，可以知道，又由C及D的特性知道，﹔且。因此，整理後，可以得到

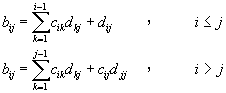                                                 (4-8.10)

由於可以利用A重複乘積計算之，cij及dij可以用下列方式計算之。

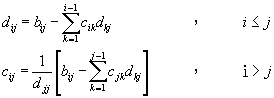                                     (4-8.11)

魯逖髾瑟的L-U分解法計算策略:

1.      將原始矩陣A放置在作業矩陣B中。

2.      將矩陣Ak分解成下三角形矩陣Lk及上三角形矩陣Rk乘積，。其中

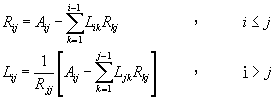
3.      將第2步驟所得到的下三角形矩陣Lk及上三角形矩陣Rk，以相反次序再組合乘積，得到Ak+1。

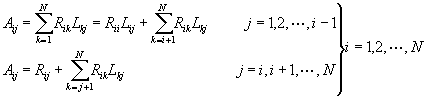
4.      由步驟2及步驟3所得到的下三角形矩陣Lk，計算下三角形矩陣的乘積矩陣。

5.      重複步驟2至步驟4，直到下三角形矩陣Lk的元素和小於某一很小的界限值Eps(2)，視為計算已收斂。

6.      矩陣A的特徵值(Eigenvalue)即為上三角形矩陣Rk的對角線元素。

7.      利用類似高斯消去法最後求解的方式，計算所得到轉化矩陣B的特徵陣列(Eigenvector)。

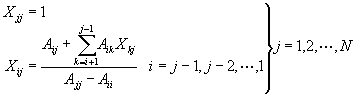
8.      最後再計算原矩陣的特徵陣列。

 

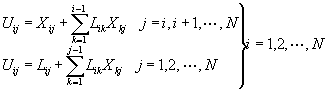
參考文獻

1.   Stark, P. A. “Introduction to Numerical Methods”, New York: Macmillan, (1970).

2.   Dorn, W. S., and D. McCracken, “Numerical Methods with FORTRAN IV Case Studies” John Wiley, (1972).

3.   Fox, L., “An Introduction to Numerical Linear Algebra” Oxford Univ. Press, (1964).

4.   Finlayson, B. A., “Nonlinear Analysis in Chemical Engineering”, (1980)

5.   Villadsen, J., and M. L. Michelsen, “Solution of Differential Equation Models by Polynomial Approximation”, Prentice Hall. (1978)

6.   Rutishauser, H, “Solution of Eigenvalue Problems with the L-R Transformation”, National Bureau of Standards, Appl. Math. Series, Vol. 49, pp. 47-81, (1958)

 

回首頁     回第二部     下一章