以便進行設計計算

第三章                          數據插值法

工程科學是一種對經驗及資料依賴性相當高的科學，工程師或研究人員時常需面對大量的圖、表，讀取資料，以便進行設計計算。表3.1的關係、蒸汽表、黏度與溫度關係表、熱傳導係數與溫度關係表、溫溼度表等，都是以類似的方法表現。但在實際使用時，表列值並不一定恰好是我們所要讀取的數值，例如，要從表3.1讀取溫度56.4 ℉，壓力為82.3 psia時的體積，就必須借助於適當的近似方法。這種在表列數據範圍內求出近似值的方法稱為插值法（Interpolation）。若需藉表列數據求出表列數據範圍以外的近似函數值，則使用外推（Extrapolation）近似法。

插值法利用數學語言描述，可簡述如下：假設存在一函數F，為自變數x、y、z、……之函數；

                                                                                      (3-1)

此函數在某些特定點為的函數值為已知；現在希望由這些點的函數關係，求一未知點之函數值。

為了說明近似法的原理，首先我們假設此函數只有一個自變數x，即函數關係為；且已經知道有n+1個已知點的函數對應關係，分別為。通常，函數可利用多項式、三角函數或指數函數等來表示。若以多項式來表示函數，即

                                          (3-2)

如果利用n+1個已知的數據，代入以上的多項式，可以得到n+1個線性聯立方程式，原則上應該可以求得n+1個變數的解。然後，利用所求得的近似方程式，即可求得在至範圍內其他各點的函數值。但是，如果數據點數很多的時候，這種處理方式將會變得非常費時，且計算所引進的誤差也將變得甚為可觀，因此，實際上並不是一種有效率的方法。

        本章將引介幾種常見的插值法，說明程式設計方法，並以實際工程問題說明其應用。

第一節           線性插值法

假設函數在與間近似於成線性關係,如圖3.1所示。當 很小時，或函數變化較緩和時，假設線性函數關係通常是相當合理且誤差相當小的，此時，若希望找出介於xi及xi+1間的一個x值之函數值，則可利用以下直線方程式計算之：

                                                   (3-1.1)

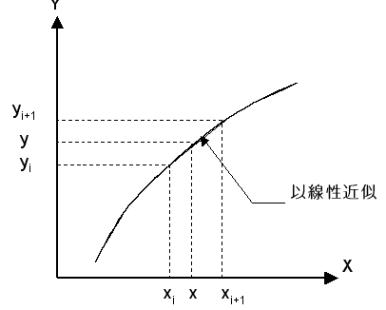
圖3.1  線性插值法

第二節           拉格蘭奇內插法

任何一個n次多項式函數都可以利用拉格蘭奇多項式(Lagrange Polynomial)表示，因此，若有已知的n + 1個數據點，可利用拉式多項式作近似，以求得中間任何一點之數值，這種方法即稱為拉格蘭奇內插法(Lagrange Interpolation)。

利用根據前述，若有已知的n + 1個數據點(x0,y0)、(x1,y1)、….、(xn,yn)，則我們可找到一個n次多項式通過這些點，亦即函數可以表示成以下的多項式：

                       (3-2.1)

由於y為x之n次多項式，因此，可將ｙ寫成n + 1個x的n次多項式之線性組合：

                                                                                    (3-2.2)

其中假設多項式均為x之n次多項式。且假設正交函數除了在第i點以外，其餘各點處其函數值均為零；且在第i點的函數值為1，亦即

                                                                                (3-2.3)

由於，考慮在第k點時，若將方程式（3-2.3）代入（3-2.2），得到

                                              (3-2.4)

其中k可以是0至n的任一自然數，故可知方程式（3-2.2）可通過所有的已知數據點。

由於為一n次多項式，且由方程式（3-2.3），可以知道由x0，x1，……至xn的n+1個點中，除了xi以外，其餘的xj值都是方程式之根，故可假設為一常數係數與 之乘積。

                     (3-2.5)

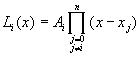
由於，代入上式，經整理後可以得到

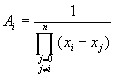
                          (3-2.6)

故由方程式(3-2.5)及(3-2.6)整理後，可將拉格蘭奇多項式寫成

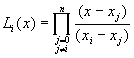                                                                               (3-2.7)

將上式代入方程式(3-2.2)，可得拉格蘭奇內插方程式為

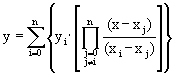                                                                     (3-2.8)

利用上式，由輸入的n+1組數據點(x0,y0)、(x1,y1)、….、(xn,yn)，代入上式即自動產生一個n次多項式。將任何x值代入此多項式中，即可求得對應的函數y值。

拉格蘭奇內插法(3-2.8)由於本身運算重複性高，相當容易編寫成計算機程式，但是其缺點是每次計算都需重複作相同項次之計算，所需時間較長。此外，如果設定多項式的階次過高，有時會使函數變成波動形式，而使內插結果產生嚴重誤差，因此，使用上應該要小心。

第三節           三次弧線內插法

線性內插法執行速度雖然快速，但只適用於曲率非常小的函數或極小的區域範圍作內插。拉格蘭奇內插法雖然可以自在地調節多項式次數，以得到適當的準確度，但這種內插法最大的缺點是每次作內插計算時，均需一再的重複計算值，因此，執行效率較差。

對於一個連續而且可微分的函數，假設我們希望在封閉區間[a, b]內，利用低次多項式，以階段方式來作為他的近似函數，理論上應該也可以得到相當好的結果。

假設已知數據基準點的範圍為，其對應的每一個點的函數值分別為 。在[a, b]區間內，假設存在n個低次多項式近似函數為，其中，且。則我們希望在[a, b]內之任何x值，多項式近似函數的一次及二次導函數（微分）均為連續函數，並滿足以下n+1個條件。

                                     (3-3.1)

在[a, b]所分割成的每一個小區間中，假設都等於三次多項式，其中下註標3表示三次多項式，因此，其二次導函數即為一線性方程式，可以寫成及的線性組合:

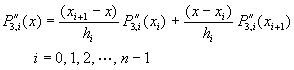                                       (3-3.2)

其中；且及均為常數。將方程式(3-3.2)積分兩次，得到

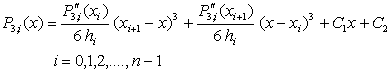              (3-3.3)

其中 為積分常數。由於通過及兩點，故

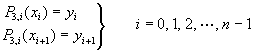                                                 (3-3.4)

將上式代入方程式(3-3.3)，求解，經整理後，得到為

 

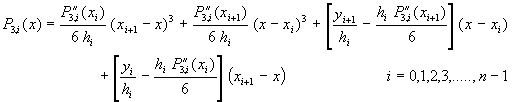
                                                                                                                (3-3.5)

由於前述之一次導函數為一連續函數，亦即

                                                 (3-3.6)

將方程式(3-3.5)對作一次微分，並利用上式條件加以整理以後，可以得到以下n-1個差分方程式:

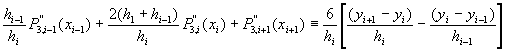
                                                                                       (3-3.7)

將方程式(3-3.7)改寫成矩陣形式，可以得到

                                                                                                                                      (3-3.8)

或可以寫成

                                                                 (3-3.9)

方程式(3-3.9)中，共有n+1個未知數，但總共只能寫出n-1個方程式。因此，必須再加上兩個已知條件，方程式(3-3.9)才能解出所有的未知數。假設所加入的兩個已知條件為端點條件及﹔通常使用的端點條件可分為三類:

(1)                假設三次弧線近似方程式於接近兩端點時，趨近於直線(即二次微分等於零)，即

(2)                假設三次弧線近似方程式於接近兩端點時，趨近於拋物線(即二次微分等於定值)，即

(3)                假設三次弧線近似方程式於接近兩端點時，其二次微分可用往內二點的二次微分作線性外插。即為及之線性外插，為及之線性外插。即

 

以第一種端點條件為例，，代入方程式(3-3.8)，則第一個方程式及最後一個方程式分別變成:

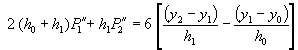                                      (3-3.10)

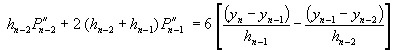              (3-3.11)

由於，在上式中已自然消去，方程式 (3-3.8)中可去掉第一項及第n+1項，成為；因此，係數矩陣可改寫成方陣:

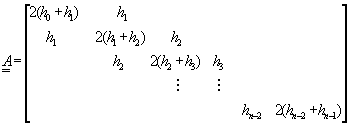                   (3-3.12)

同理，利用第二種端點條件，可以整理得到方陣:

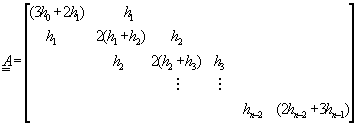                 (3-3.13)

利用第三種端點條件，可以整理得到方陣:

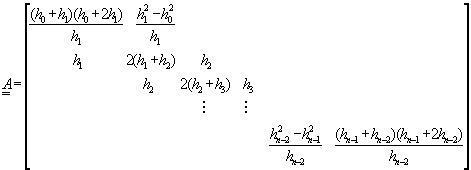
                                                                                                             (3-3.14)

由於係數矩陣均成為三對角線矩陣(Tridiagonal Matrix)，因此，求解及儲存都相當方便，其程式設計方法可以參考本書第四章有詳細討論。三次弧線內插法的程式設計請參考本書範例3.4，執行方法歸納如下：

1. 先定義端點條件；

2. 求解方程式(3-3.9)得到；

3. 再利用方程式(3-3.5)可進行內插計算。

例3.3 三次弧線近似法

試利用三次弧線法表示下列數據。表中數據真正關係式為

 

表3.4

I

X (I)

Y (I)

0

0

-5

1

1

-3

2

2

11

3

3

49

4

4

123

解：  利用端點條件1: ，代入方程式（3-3.9）得到

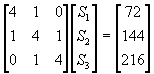
故得到。

利用端點條件2: ，則聯立方程式為

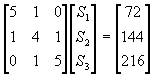
故得到。

利用端點條件3: 為及之線性外插，為及之線性外插，則聯立方程式為

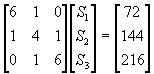
故得到。

將原方程式微分兩次，得，將x值代入，恰與利用端點條件3所得結果一致。

第四節     二度空間線性內插

考慮含有兩個自變數x，y的函數f：

                                                                                            (3-4.1)

假設我們已有個函數值，對應m個及n個值的所有組合。為了方便起見，將建成一個二次元的數據表（如表3.1）。本節所要探討的是如何由表中數據作內插，以求得任意x、y值的函數近似值。

        考慮線性內插，令，且，如圖3.2所示。圖中○符號表示已知的數據點。首先由至和至分別作線性內插，得到A及B兩點的函數的近似值及﹔然後，再作線性內插，即可得最後的近似值。

 

 

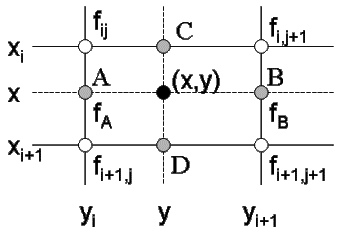
圖3.2  二度空間線性內插

根據方程式（3-1.1），由至作線性內插，可以得到

                                                            （3-4.2）

同理

                                                   （3-4.3）

再由A點至B點作線性內插，得

                                                     （3-4.4）

將（3-4.2）及（3-4.4），整理後，得到

（3-4.5）

其中；。

參考文獻

1.   Perry, R. H. and C. H. Chilton, “Chemical Engineers’ Handbook”, McGraw-Hill, (1973).

2.   Eckert, E. R. G. and R. J. Goldstein, “Measurement in Heat Transfer” Hemisphere, (1976).

3.   Carnahan. B., H. A. Luther, and J. O. Wilkes, “Applied Numerical Methods” John Wiley, (1969).

4.   Dorn, W.S., and D. D. McCracken, “Numerical Methods with FORTRAN IV Case Studies”, John Wiley, (1972).

5.   “Encyclopedia of Chemical Technology”, Vol.2, 2nd ed., New York, Wiley, (1963).

 

回首頁     回第二部     下一章